- Définition de la racine carrée ; les carrés parfaits entre 1 et 144.
- Théorème de Pythagore et réciproque
Définition 1 :
Dans un triangle rectangle,
l’hypoténuse est le côté du triangle opposé à l’angle droit.
Remarque 1 :
L’hypoténuse est toujours le côté le plus long.
Propriété 1 :
Théorème de Pythagore :
Si un triangle est rectangle , alors le carré de la longueur de son hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Exemple 1 :
Soit le triangle ABC rectangle en A ([BC] est donc l'hypoténuse),
alors BC²=AC²+BA².
Exemple 2 :
Soit DEF un triangle rectangle en E , EF=5 et FD =13 , que vaut la mesure de [DE]?
On sait que le triangle DEF est rectangle en E . [DF] est l'hypoténuse.
D'après le théorème de Pythagore, on a : $DF^2=EF^2+ED^2$
d'où $13^2=5^2+ED^2$
$169=25+ED^2$
$ED^2=169-25$
$ED^2=144$
$ED=12$
Pour trouver la longueur de DE, il faut chercher le nombre positif qui au carré vaut 144.
On utilise la racine carrée $\sqrt{}$.
$DE=\sqrt {144}=12$
Remarque 1 :
Le théorème de Pythagore sert à calculer une longueur lorsque l’on connaît 2 côtés.

Définition 1 :
Soit un nombre $a$ positif. $\sqrt {a}$ est le nombre positif dont le carré vaut a.
Dans l’exemple précédent DE²=144 donc $DE =\sqrt {144}=12$
Exemple 1 :
$5^2=25$ donc $\sqrt{25}=5$.
Définition 2 :
On appelle
carré parfait , un nombre entier positif dont la racine carrée est entière.
| Nombre entier | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Carré Parfait | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 |
IV
Déterminer si le triangle est rectangle ou non
Exemple 1 :
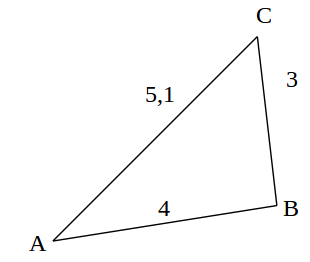
Soit un triangle ABC tel que AB=4 , BC =3 et AC=5,1.
Le triangle est-il rectangle?
On sait que [AC] est le côté le plus long donc pourrait être l’hypoténuse.
Calculons d'une part AC² et d'autre part AB²+CB².
$AC^2=5,1^2=26,01$
$AB^2+BC^2=4^2+3^2=16+9=25$
Donc
$AC^2 \ne AB^2+BC^2$
L’égalité de Pythagore n’est pas vérifiée donc le triangle n’est pas rectangle.
Exemple 2 :
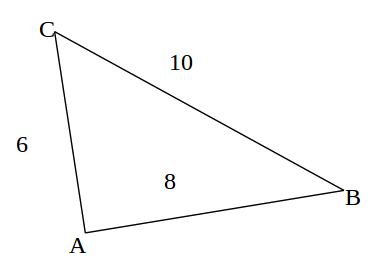
Soit un triangle ABC tel que AB=8 , BC =10 et AC=6.
Le triangle est-il rectangle?
On sait que [BC] est le côté le plus long donc pourrait être l’hypoténuse.
Calculons d'une part BC² et d'autre part AB²+CA².
$BC^2=10^2=100$
$AB^2+AC^2=8^2+6^2=64+36=100$
Donc
$BC^2 = AB^2+AC^2$
L’égalité de Pythagore est vérifiée donc le triangle est rectangle en A.
Remarque 1 :
L’égalité de Pythagore permet de montrer si un triangle est rectangle ou non.