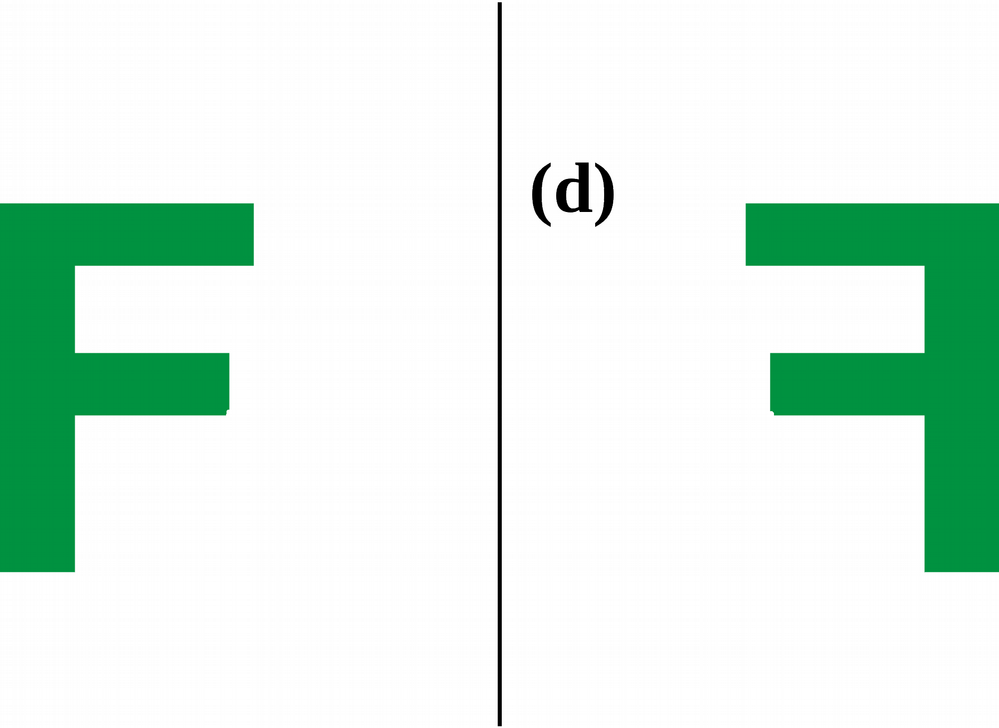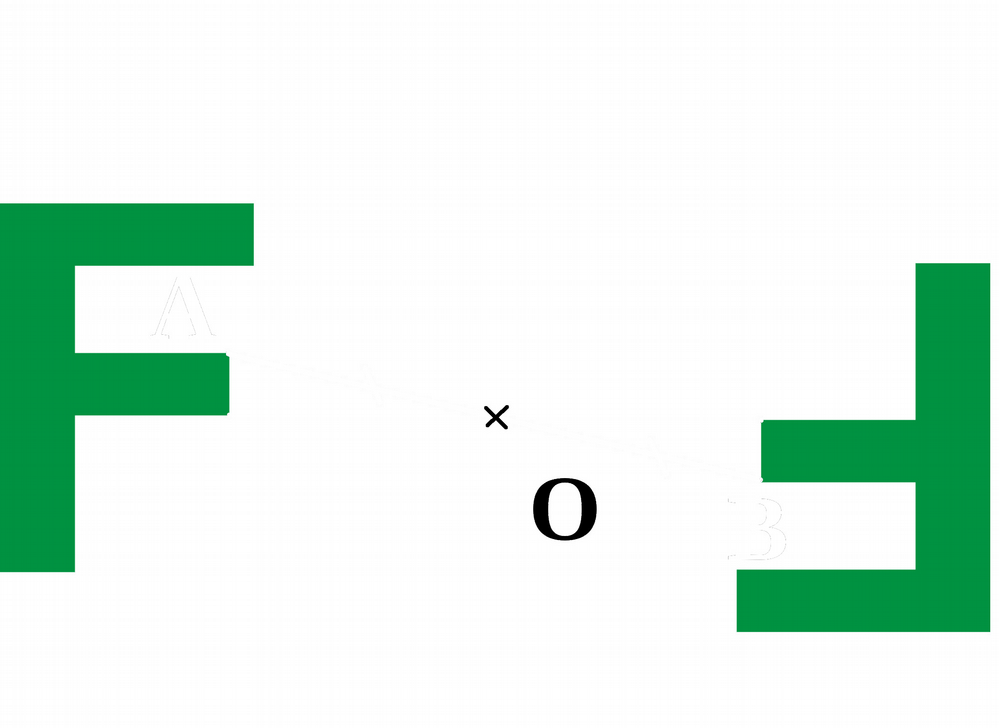- Comprendre l’effet d’une translation, d’une symétrie (axiale et centrale), d’une rotation sur une figure.
Définition 1 :
Transformer une figure par une symétrie axiale, c’est créer l’image de cette figure par pliage le long de l’axe.
Voir chapitre symétrie axiale
Exemple 1 :
Voici le symétrique de la lettre F par rapport à la droite (d)
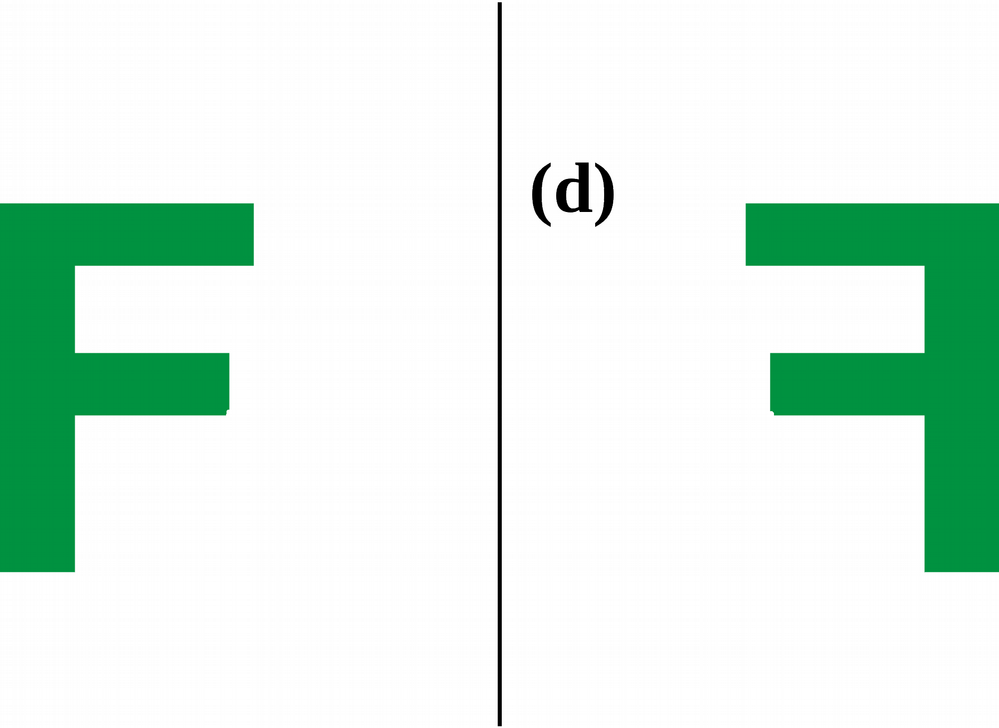
Définition 1 :
Transformer une figure par symétrie centrale, c’est créer l’image de cette figure par un demi-tour autour du centre.
Voir chapitre symétrie centrale
Exemple 1 :
Voici le symétrique de la lettre F par rapport au point O.
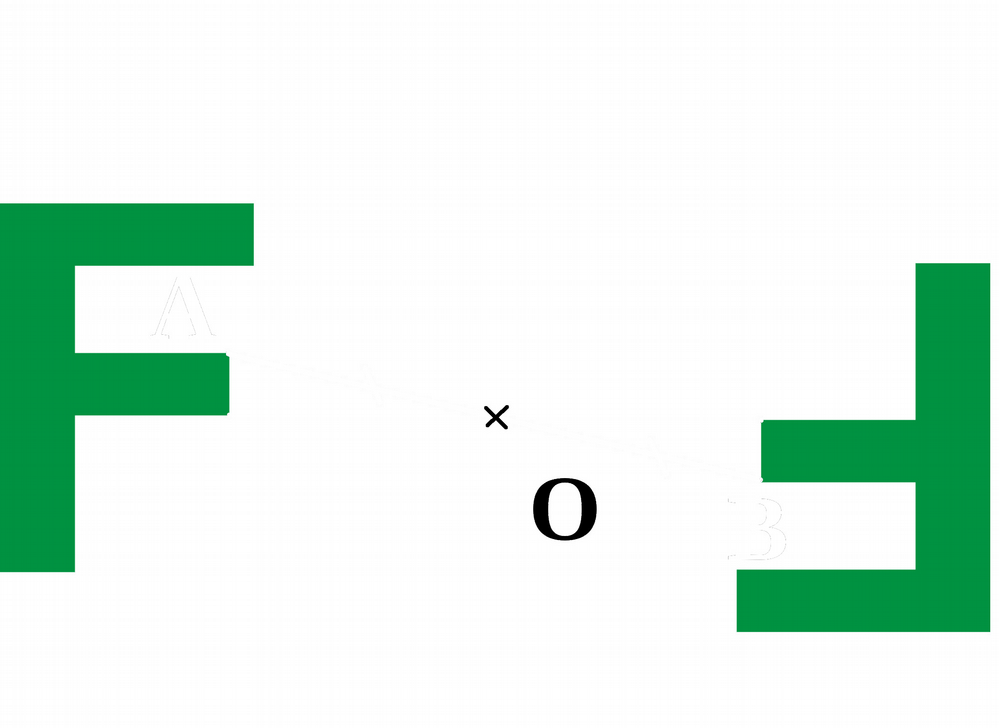
Définition 1 :
Transformer une figure par translation, c’est créer l’image de cette figure par rapport à un glissement d’un point à un autre point.
Exemple 1 :
Voici la translation de la lettre F par un glissement du point A vers le point B.

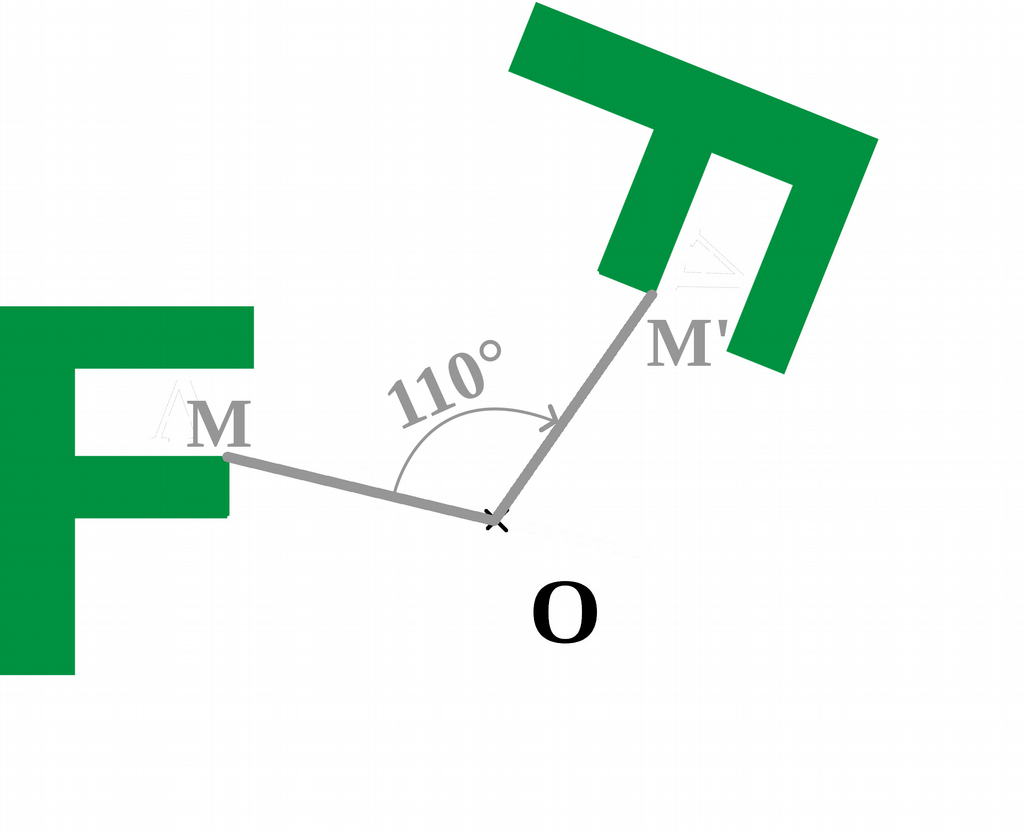
Définition 1 :
Transformer une figure par rotation, c’est créer l’image de cette figure par une rotation autour du centre suivant un angle donné.
Exemple 1 :
Voici la rotation de la lettre F par rapport au point O suivant un angle de 110°.
Remarque 1 :
La rotation autour d’un centre O d’un angle de 180° correspond à une symétrie centrale de centre O.