- Reconnaitre une situation de proportionnalité ou de non-proportionnalité.
- Résoudre des problèmes de recherche de quatrième proportionnelle.
- Résoudre des problèmes de pourcentage.
- Coefficient de proportionnalité
Définition 1 :
Un tableau est de proportionnalité si pour passer de la première ligne à la seconde ligne, on multiplie toujours par le même nombre, ce nombre est alors appelé
coefficient de proportionnalité.
On dira que les deux grandeurs, correspondant à chaque ligne, sont
proportionnelles.
Exemple 1 :
À une station-essence, le sans-plomb 98 est vendu à 1,34€ le litre. La quantité d’essence et le prix sont donc proportionnels.
On a donc un tableau de proportionnalité :

II
Compléter un tableau de proportionnalité
Exemple pour expliquer les méthodes.
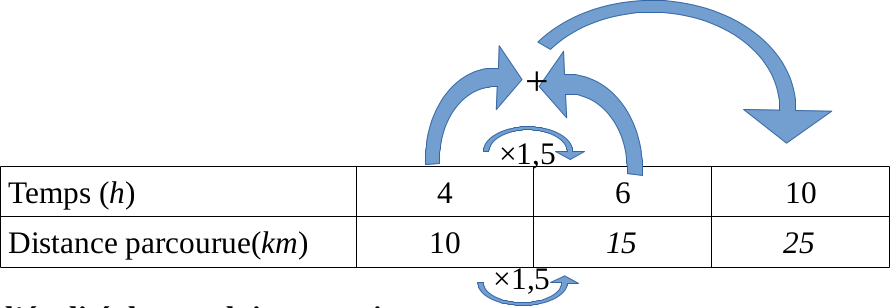
Voici un tableau de proportionnalité à remplir.

En 4 heures, nous parcourons 10 km.
En 1 heure, nous parcourons donc 4 fois moins de distance qu'en 4 heures à savoir 10 :4=2,5 km
En 6 heures, nous parcourons donc 6 fois plus de distance qu’en 1 heure à savoir 2,5×6=15 km
En résumé :

B
Avec le coefficient de proportionnalité
On cherche par quel nombre on multiplie 4 pour obtenir 10. 4×...=10 C’est le nombre ${10 \over 4 } = 2,5$
6×2,5=15

C
En utilisant les propriétés du tableau de proportionnalité
Propriété 1 :
Dans un tableau de proportionnalité, on peut :
- multiplier/diviser une colonne par un nombre
- ajouter/soustraire des colonnes entre elles.
Définition 1 :
Sur un plan, les longueurs sont proportionnelles aux longueurs réelles. Le
coefficient permettant de passer des longueurs réelles aux longueurs du plan (dans la même unité
de mesure) s’appelle
l’échelle du plan.
Exemple 1 :
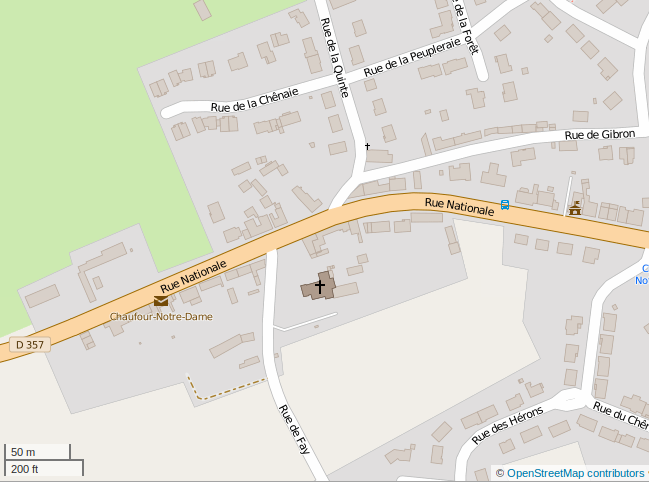
Ici la carte ci-contre est à l’échelle 1/5000 (ou $1 \over 5000$).
Cela signifie que les longueurs réelles sont 5 000 fois plus grandes que sur le
plan.
En effet,1 cm sur le plan équivaut à 5000 cm dans la réalité, soit 50m.
Définition 1 :
Un pourcentage de t % traduit une proportion de $t \over 100$.
Appliquer un taux de t% à une quantité revient à calculer $t \over 100$ de cette quantité.
Exemple 1 :
Dans une classe de 30 élèves, 20 % ont pris l’option Latin.
Je vais donc calculer $20 \over 100$ de $30$ :
${20 \over 100} \times 30 = 0,2 \times 30 = 6$
6 élèves ont pris Latin.
Définition 2 :
Déterminer un pourcentage revient à donner la proportion
dont le dénominateur est
100.
Exemple 2 :
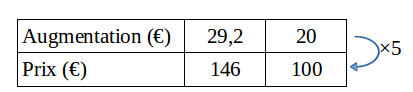
Un manteau coûtait 146€ et a augmenté de 29,20 €. Quel est le pourcentage d’augmentation?
La proportion de l’augmentation est de $29,20 \over 146$.
Or ${29,20 \over 146 }= 0,2 = {20 \over 100} = 20$%
Le manteau a augmenté de 20%.
On peut aussi utiliser un tableau de proportionnalité :