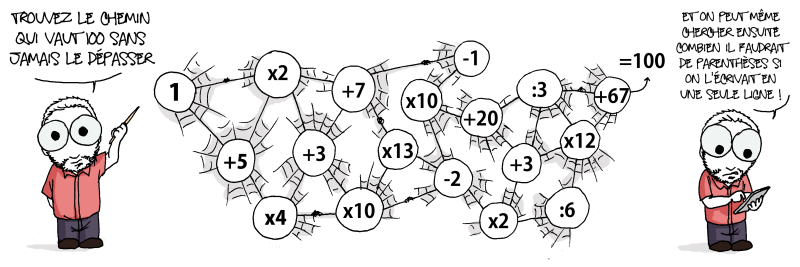
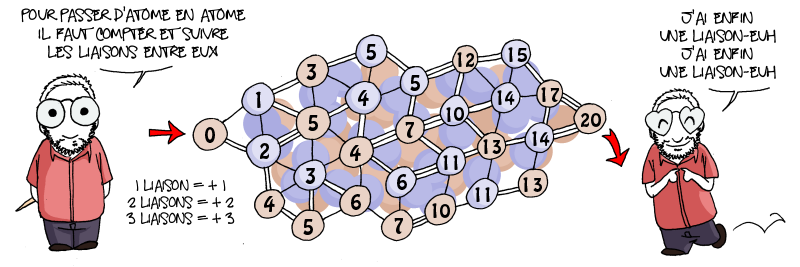
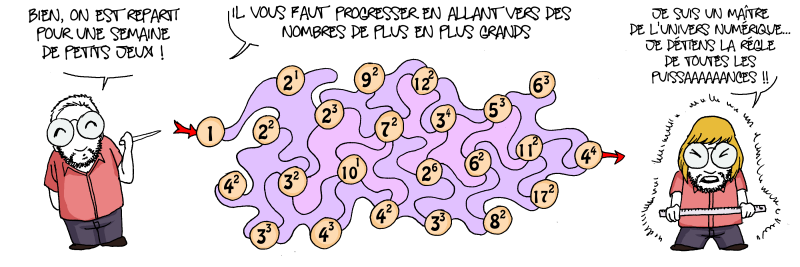
Voici la suite des petits jeux qu’Evan nous offre.

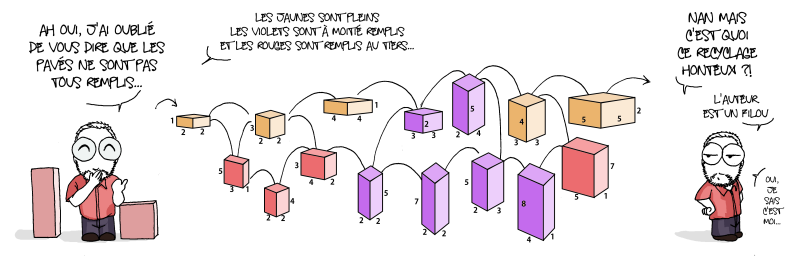
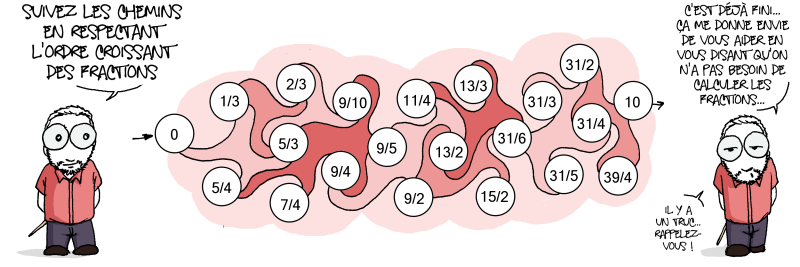
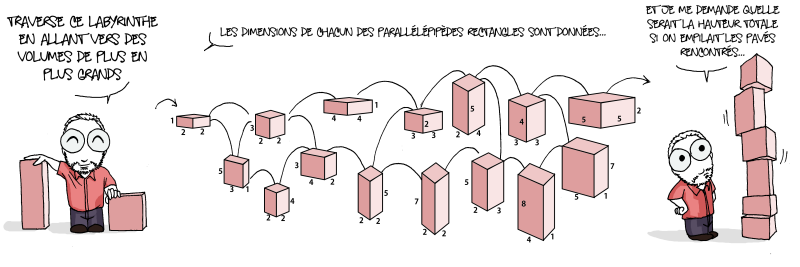
Ceux-ci ont accessibles aux élèves de 6e, le premier concerne les volumes et les proportions (donc plutôt vers la 2e moitié de l’année pour une meilleure aisance). Le second parle de l’ordre entre les fractions, il peut se faire dès la 6e… Effectivement comme le dit le dessin, il n’y a pas besoin de calculer les fractions, par simple déduction en comparant à un entier (plus grand que 2 et l’autre est plus petite), on y arrive.

Alors vous y arrivez?

Ils viennent du site evanetc.free.fr .

Source : http://evanetc.free.fr/index.php?page=888 http://evanetc.free.fr/index.php?page=887

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :