Bonjour à toutes et tous!

Voici un petit générateur de fleurs multiplicatives !

On choisit si on veut une fiche complète d’une table donnée ou on peut faire un mix entre les tables (à raison de 6 fleurs par page).

Pourquoi?

L’idée est de changer de la forme classique 11×6=… à compléter, qui peut parasiter l’apprentissage, l’enchaînement « textuel » peut entraîner une fatigue et également un brouillage de la restitution (trop de texte partout …)

12 fleurs sur une page correspond à 72 calculs et pourtant la fiche est aérée et on fatigue moins, on ressent également une progression fluide par paquet de 6 calculs (1 fleur).

Changer la forme de l’exercice permet également de faire « croire » inconsciemment » que l’on fait un autre type d’exercice, on relance la motivation.

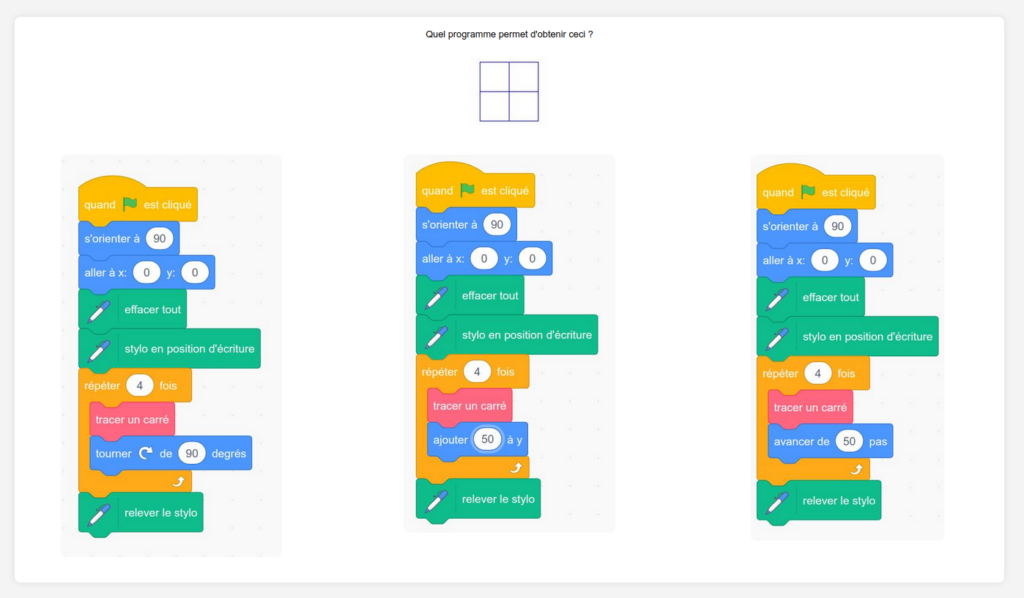
Voici trois exemples de générations :

C’est par ici : https://www.mathix.org/table-fleur/index.html

Bonjour à tous!

Voilà un projet d’animation reprise à partir des dessins que je faisais en classe (hormis les « coucous,chuis là » qu’il m’arrive de rajouter sur les bonhommes pour égayer les ), je reprends l’écriture en décomposition décimale pour faire émerger la notion de valeur approchée.

Comprendre et faire émerger la « méthode » consistant à regarder le chiffre  » d’après » pour voir quelle valeur est la plus proche… Car cette méthode parfois lâchée auprès des élèves comme cela à ses limites.

Donc je passe souvent par la représentation d’un bonhomme qui fait des pas pour approcher la valeur attendue. Par exemple pour 123,23, le bonhomme va commencer par faire des pas de 100 (un seul), puis 2 pas de 10 … (on devine ainsi la décomposition décimale).

L’idée que les élèves puissent s’imaginer avancer pas à pas, revenir à une sorte d’approche par la proprioception.

Mais quand il a fini de faire des pas de 1, on peut se poser la question s’il est plus proche de 120 (où il était arrivé en faisait des pas de 10) ou de 130 (s’il avait continué) ainsi on peut décider quelle valeur est la plus proche à la dizaine près. (balayant au passage que pour les valeurs approchées la précision n’est pas forcément à l’unité, au dixième près etc.)

Rien ne vaut une petite vidéo en action.

Voici le lien pour accéder à l’animation (c’est la première version).

https://www.mathix.org/anim_arrondir/

Bonjour à tous!

Voici la 5e version (qui a donc très rapidement évolué depuis samedi)

• J’ai donc ajouté les translations et symétries axiales (horizontal et diagonal) !
• D’autres figures sont possibles (comme le drapeau, le rectangle, un poisson ou un quadrilatère quelconque)

J’ai grossi le quadrillage pour l’impression.

C’est donc toujours à la même adresse !

https://www.mathix.org/transformation/

Bonjour à tous!

Après un contrôle un peu compliqué je me suis mis en tête de faire un exerciseur couplé à un générateur d’exercices sur des transformations sur un quadrillage.

Je suis plutôt content du résultat surtout pour les homothéties (qui était ma volonté première).

L’exerciseur propose des situations sur un quadrillage et on doit dessiner le rectangle image.

Il nous indique quand on a tort.

et quand on a raison :

Et puis si on en a marre on peut demander la solution.

Si on veut un format papier, on peut également générer une feuille avec 4 situations générées aléatoirement sur le thème voulu (homothétie, symétrie centrale ou rotation) avec en 2e page la correction (dans mon idée j’imagine en recto-exo verso-corrigé).

Voici un pdf généré avec le programme sur l’homothétie :

Le programme est disponible là : https://www.mathix.org/transformation/