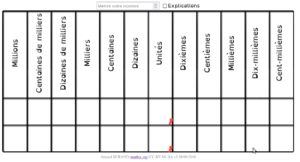
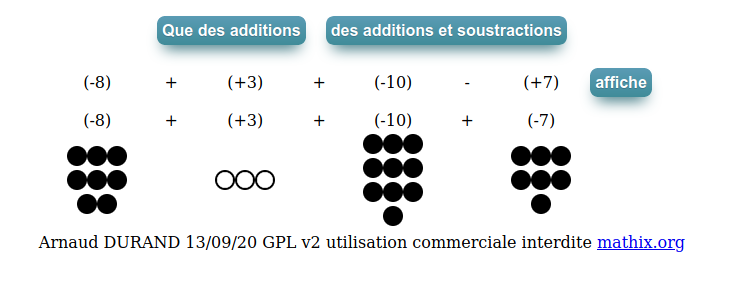
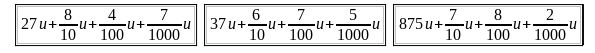Bonjour à tous
Je profite que mes élèves planchent sur le brevet pour terminer un outil qui aurait été bien pratique cette année : une caméra document.
Je m’explique, nos deux salles de classe de mathématiques sont munies de caméra document, c’est un outil super pratique pour voir des productions d’élèves ou même afficher un exercice de livre pour le commenter etc…
Bref, on est super content de cet outil et franchement le besoin se ressent quand on ne l’a pas.
Alors avant je passais par mon téléphone et je m’envoyais par mail la photo pour « rapidement » avoir l’image à projeter, je dis rapidement en fait ça prenait pas mal de temps, beaucoup trop!
Donc j’ai concocté un outil qui permet rapidement de prendre une photo et de l’avoir sur l’ordinateur et cela sans que le serveur ne garde les images, dès qu’elle est lue, hop elle est supprimée du serveur (pas de soucis de confidentialité).

Alors il existe une alternative qui est ChingView2, qui est nettement plus étoffée (on peut écrire sur les images etc… on peut gérer l’affichage de l’ordinateur avec le téléphone) , mais il vous faudra un compte, contrairement à moi où cela marche directement.
Alors comment ça marche ?
J’ai essayé de faire un truc simple !
On se rend ici :
https://www.mathix.org/macamdoc/

On observe 2 parties :
Le QRcode et le lien « Ma session ».
Le Qrcode doit être scanné par le téléphone portable qui servira de caméra, le lien « Ma session » doit être cliqué sur l’ordinateur qui vidéoprojetera l’image.
Sur l’ordinateur
Si vous cliquez sur le lien alors que vous n’avez pas encore pris de photos vous aurez simplement un message indiquant qu’il n’y a pas de photo et un rappel du QRCode à scanner avec le téléphone portable.

Sinon vous aurez directement l’image qui s’affichera (en prenant le plus de place).

Vous avez trois boutons :
- Le premier permet de rafraîchir l’image si vous avez pris une autre photo
- Le second permet de faire pivoter l’image
- Le 3e permet de télécharger l’image sur l’ordinateur
Le bouton rafraîchir :
Admettons que vous voulez rafraîchir l’image mais que vous n’avez pas pris de photos (en théorie il n’a plus d’image à afficher car elle a été supprimée), il refusera de rafraîchir avec un message indiquant qu’aucune nouvelle photo n’a été prise et restera à afficher l’image.

Et si vous avez pris une nouvelle photo il l’affichera.

Le bouton pivoter
il pivote tout simplement l’image de 90°.

Le bouton Télécharger
Il permettra d’enregistrer l’image.
Sur le téléphone :
Dès qu’on scanne le Q-code, on doit autoriser l’utilisation de la caméra, on voit tout simplement ce que filme la caméra.

il suffit de cliquer sur l’image pour prendre la photo.

L’image se fige alors et 2 boutons apparaissent.
Celui de gauche permet de reprendre la photo, si elle n’est pas bien.
Celui de droite permet d’envoyer l’image sur le serveur.
Dès qu’on envoie, un message indique si l’image est prête, et invite l’utilisateur à cliquer sur le bouton pour rafraîchir sur l’ordinateur!