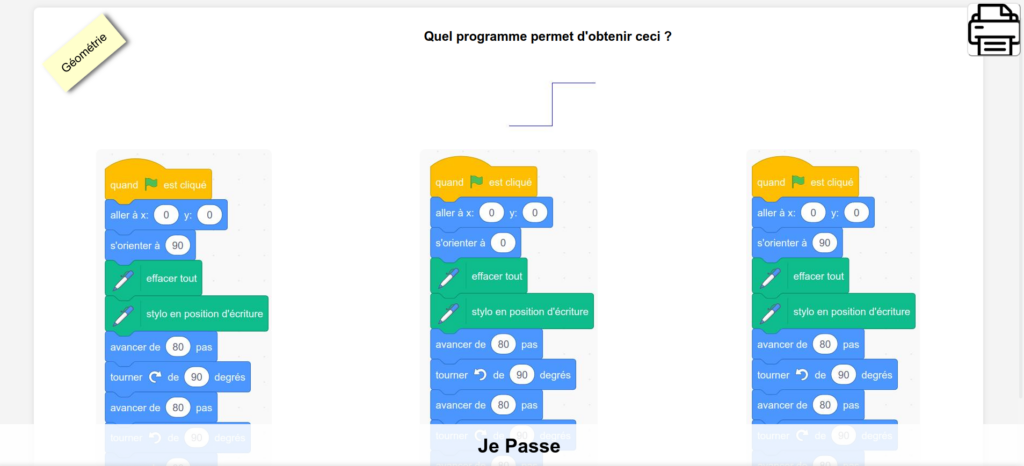
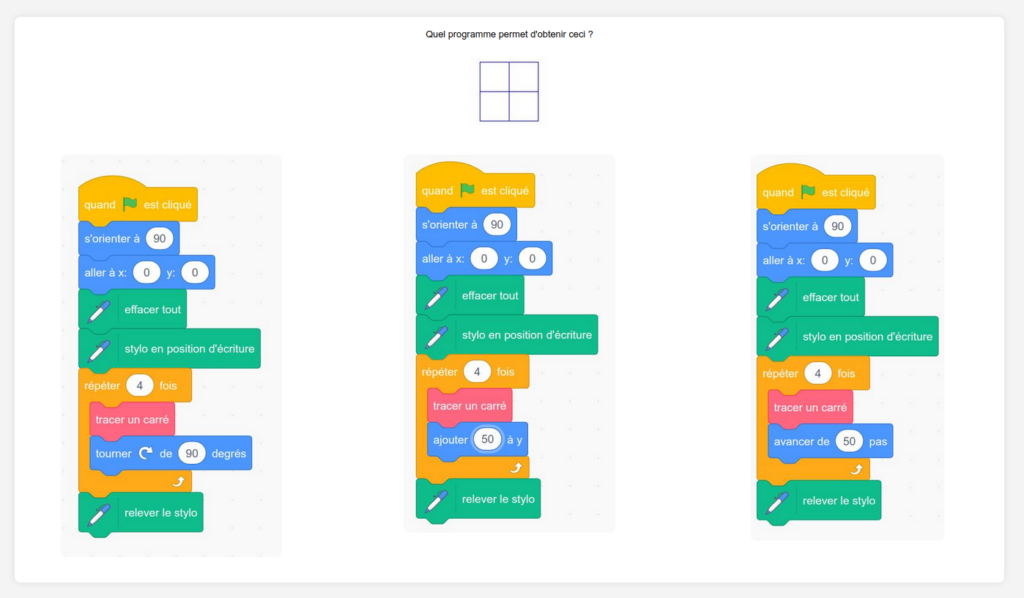
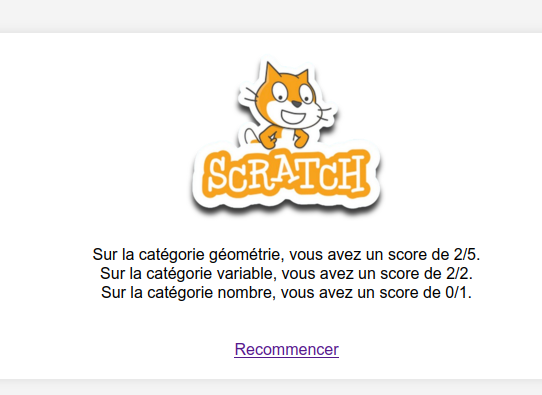
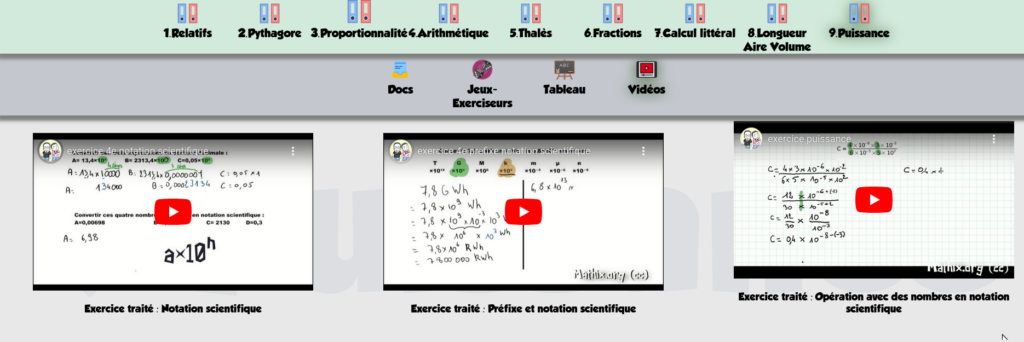
Bonjour à toutes et tous!

Voilà une petite erreur qui peut faire sourire, elle est intéressante dans le fait qu’elle présente d’une manière les conditions d’application du théorème de Thalès (en faisant une erreur), en effet on trouve souvent les conditions du type droites parallèles et points alignés et un peu moins Deux droites sécantes et deux droites parallèles.
Après de là, à l’exploiter en classe pour une activité avec les 4e ou 3e…
Je la trouve juste rigolote. 🙂
Edit : Alors pour ceux que cela intéresse. Le rapport de 3 parallèles avec deux séantes n’est pas le théorème attribué à THALES, mais était connu de ce dernier. L’attribution du nom de THALES au théorème est du XIXe siècle.