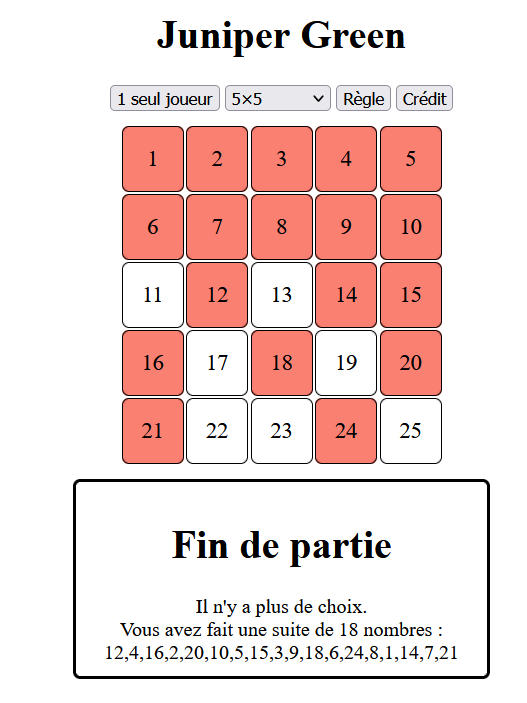
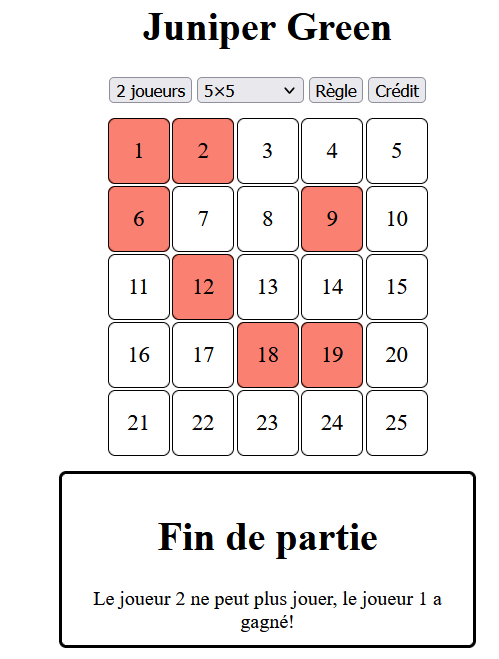
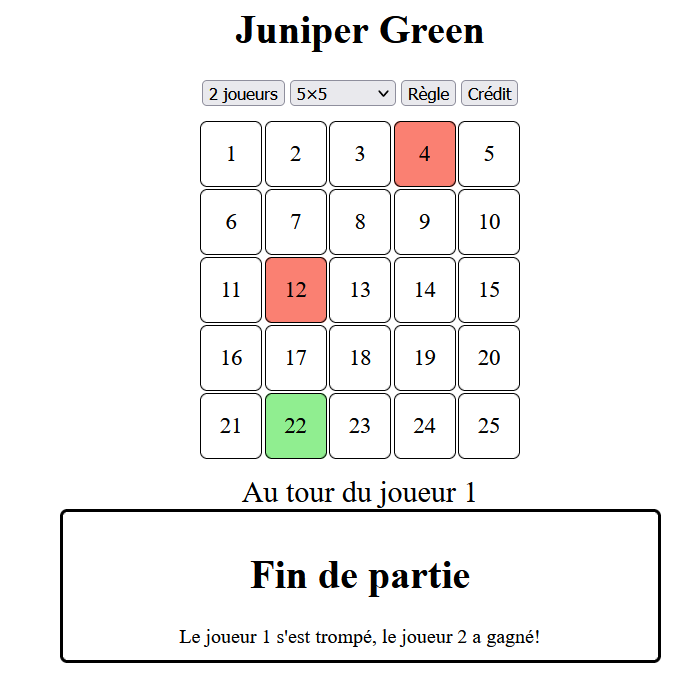
Bonjour à tous !!
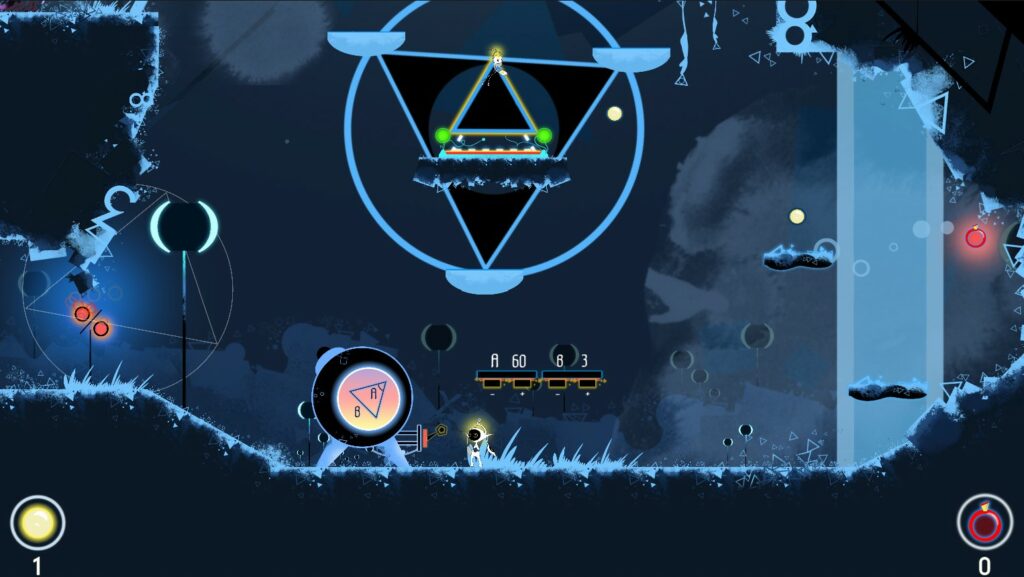
Voilà un jeu que j’ai trouvé juste extra-ordinaire!
Et le seul bémol, c’est que le jeu ne propose pas à deux joueurs de jouer sur le même support.
Donc ni une ni deux, je me suis mis en tête de travailler sur un mini-site html/js qui le permette.
Outre le fait que c’est bigrement moins consommateurs de ressources, il n’y a pas besoin d’installation !
Le chargement est quasi-instantanné et on peut jouer à deux sur le même support!
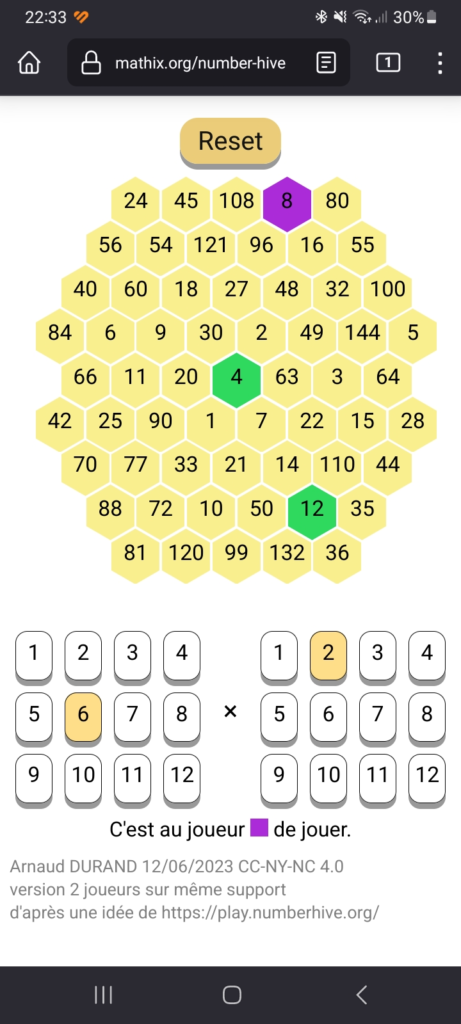
Qu’est-ce que j’ai galéré sur la création de la grille! Mais je ne suis pas peu fier du résultat !
Ça rend trop bien sur le smartphone !!
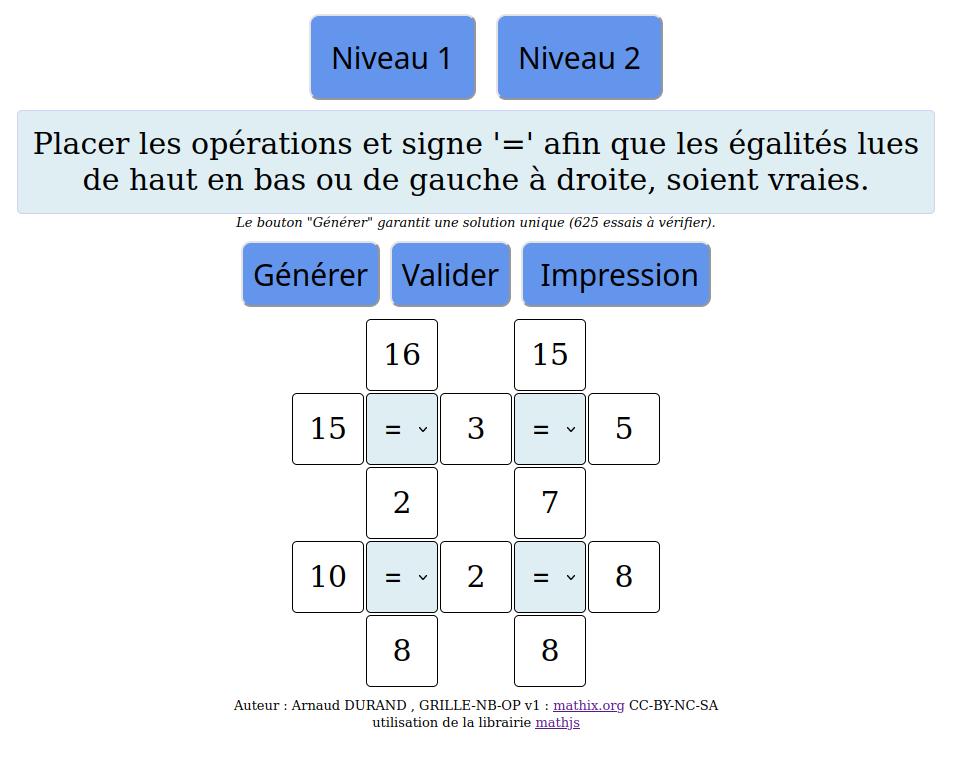
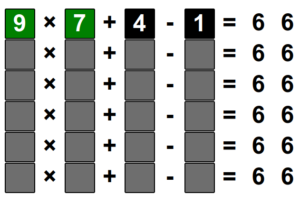
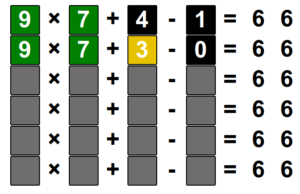
Ce jeu est idéal pour faire travailler les tables de multiplications (et la décomposition des nombres en produits !
Les grilles sont générées de manière aléatoire.
La règle est simple :
- vous changez un des deux facteurs, et cela coloriera automatiquement la case dont le numéro est le produit des deux facteurs.
- Puis c’est à l’autre joueur de changer un des deux facteurs.
- Le premier à aligner 4 pions a gagné!
https://mathix.org/number-hive_/index.html
Je vais travailler sur des variantes (multiplication de relatifs, et voir même pour l’addition?)