Préambule : c’est mon deuxième article et je n’ai pas l’aisance ni la plume d’Arnaud, même si j’ai la même tête, la qualité laissera surement à désirer, mais ne vous arrêtez pas sur la forme mais sur le fond, en espérant vous faire découvrir et ne pas enfoncer des portes ouvertes….

Je reviens d’une formation « Briques au collège » animée par Carole Baranger et Thierry Royer (et co-construite avec Manuel Lebeugle.)

C’est ce genre de formation, où vous sortez de là et vous vous dites :

Mais c’est évident, comment j’ai pu faire sans ?

MAIS POURQUOI FAIRE ?

La manipulation des nombres par jetons ou autres est souvent développé dans le premier degré, afin de permettre aux élèves de manipuler les nombres en tant qu’objets physiques mais aussi en tant qu’objets mathématiques. Et c’est là où je trouve cela beau.

Certes, peut-être qu’à me lire, vous vous dites :  » ok, Julien, y a rien de nouveau. » Oui et non… l’utilisation n’est pas une nouveauté, mais partir de cette manipulation pour tous, peut-être un peu plus.

RECONSTRUIRE DES REPRESENTATIONS ERRONEES : Je m’appuie souvent sur l’objet pour pallier et ou remédier des représentations erronées des objets mathématiques de la part des élèves afin de les reconstruire correctement.

AIDER A REPRESENTER UNE SIUTATION CONCRETE (pas pour tous) : Des constructions de maquettes pour permettre une meilleure représentation afin d’accéder à une modélisation correcte et ainsi des raisonnements justes ( notamment pour ce problème DUDU ).

AIDER A LA MANIPULATION D’OBJETS MATHEMATIQUES :

• Des jetons pour la construction des relatifs (et l’appui de l’excellente vidéo d’Arnaud #promotion 🙂 ),
• des disques en carton avec des cordes pour effectuer leurs développées (c’est expérimentale, et la représentation est identique à l’objet).

L’accès à ces briques va faciliter grandement cette approche dans bien d’autres notions, certes j’avais mes activités, mais je n’axais pas la manipulation comme pièce centrale de l’activité.

Donc on joue manipule des objets pour ensuite manipuler jouer avec les objets mathématiques : toute la philosophie des activités de manipulation est là.

Mais comment pousser naturellement les élèves à s’émanciper de l’objet physique ?

PAR LE MANQUE.

C’est brillant, vraiment, j’ai vécu l’activité côté élève, je vous assure, le côté « euh Thierry, il manque un rouage. » et je le vois me sourire, PAF, je comprends que c’est le levier de l’activité, le moment où l’activité prend toute sa dimension mathématique : on est obligé de faire sans donc de s’affranchir du matériel.

En fait, de nombreuses activités que j’ai faites sont construites comme cela, mais pas forcement comme une construction comme telle. Ma vraie avancée, c’est cette notion de plan d’activité qui peut se dessiner dans bien d’autres dispositifs. L’attrait également des la brique, cela reste un jeu mais que l’on utilise pour du travail : J’ADORE !

Un petit exemple d’activité.

Voici la première activité ( en binôme) que j’ai construite avec deux collègues du Rallye, Armelle et Lionel (dit mon Lapin).
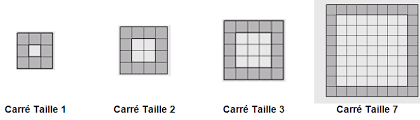
On part sur un petit modèle composé de 3 pièces, et on demande naïvement aux élèves de construire un motif deux fois plus grand puis trois fois plus grand.

ATTENTION : Il y a être vigilant sur la construction de leur représentation : le fait que nous comptions les tenons (notion d’aires) et on ne part pas sur le volume (qui fait l’objet d’une deuxième activité).

Les deux premières questions sont accessibles par le matériel, la gestion de la différentiation se fait aisément, certains se sépareront du matériel rapidement, quand d’autres devront davantage s’appuyer sur les briques pour y répondre.

LE MANQUE comme levier !

La dernière question est posée comme un DEFI car ils n’ont pas suffisamment de briques pour faire le motif 5, mais ils peuvent effectuer le motif 4 afin de confronter leurs différentes hypothèses.

Alors certes, la littérature a déjà documenté ce principe, mais de le vivre, je vous assure, c’est jouissif, alors j’ai bien envie de le faire vivre aux élèves.

Cela se passe donc en trois étapes :

1. Manipulation des objectifs physiques et observations (« Chercher ») (MOTIFS 2 et 3 )
2. Par le manque, conjecture et construction ou consolidation des objets mathématiques (MOTIF 5)
3. Vérification de la conjecture expérimentale (MOTIF 4)

Pendant la phase bilan, il est important d’asseoir leurs conjectures par un apport mathématique solide (démonstration, preuve numérique etc…) afin de ne pas être dans le « je vois, je sais ».

Je vous joins une petite vidéo (pardon Arnaud, c’est sur Youtube, mais les cahiers Péda ont choisi ce mode de diffusion…) qui quand je l’ai vue, a mis des mots sur ce que je voyais.

Bref, une petite baffe didactique

Pour finir, je vous joins ma première activité complète sur l’agrandissement en 3e.
Je vais sûrement en produire d’autres que je mettrai je ne sais où sur le site, pour ceux que cela intéresse.

Car oui, y a plein de possibilités, comme le calcul littéral. Si nous reprenons la classique activité d’Eduscol (« rien de péjoratif dans « classique », c’est juste qu’elle existait déjà quand j’ai commencé à enseigner.)

Vous voyez l’idée, tout à fait exploitable en mode LEGO.

Et avec les rouages, qui n’a jamais pensé aux Legos technics,

Je ne vais pas privilégier le LEGO à tout prix, mais cela reste une piste intéressante :

• Accessibilité aux notions facilitée par la manipulation
• Démarche scientifique (observation/conjecture/ confirmation)
• Effet WAOUH (moment fort/ moment référence)

Dans la formation, certains s’étaient orientés sur les fractions, d’ailleurs Claire Lommé nous en avait créée une il y a quelques temps très bien.

J’ai d’autres piste sur : la division euclidienne, des nombres premiers, des fractions, des volumes…

LES FREINS

J’en vois quelques-uns,

Le coût : le premier étant le matériel , j’ai privilégié le bon coin pour la une bonne base de matériel et mes enfants pour effectuer le classement ( oui c’est de l’esclavage assumé, cela m’a permis de faire des tas avec eux et de construire une représentation de la multiplication (Oui c’est dur d’être fils d’un Dudu…).
J’ai du acheter quelques boites, et surtout des boites de rangements.

Le rangement avant et après : il faut classer, avoir des rangements efficaces, ne pas perdre des pièces.

Le côté enfantin : pour du cycle 3, je n’y vois aucun frein, mais pour mes grands 3e, je me pose vraiment la question, je vois déjà mon « Tom » me regardant en mode « il nous fait quoi le Durand ? Il a craqué?!? ». J’ai un peu peur du côté soufflet, mais cela ne m’a jamais arrêter ! et en plus ils sont supers sympas, je vais tenter l’aventure, quitte à faire un flop, ils s’en souviendront 😀 je ferai sûrement un petit retour.

PS : Oui, j’écris très peu d’articles, car j’ai pas le temps, mais là, ça a été une si belle surprise, que j’ai envie de la partager.

Voici la première activité :