Bon je vais jeter un petit pavé dans la mare…
Rétrospective, Réforme 2016, on ôte le terme de « réciproque » du théorème de Pythagore, j’étais colère, car je voyais beaucoup de cohérence avec la séquence sur les droites des milieux, sur le travail de notion d’implication et réciproque.
Puis on fait avec, je parle d’égalité de Pythagore vérifiée ou non. Puis 2019 on réinsère le terme de réciproque pour Pythagore…. Grrrrrrr
Mais là je n’y trouve plus de cohérence.
C’est pas nouveau avec Ju’ on est sur un projet de rétablir des démonstrations, et donc on a fait un travail de construction des notions les unes par rapport aux autres.
Bref, donc on a fait un petit travail sur Pythagore (qui n’est pas encore fini avec des Guests de malade), et là on a commencé à réfléchir à la réciproque de ce théorème.
Comment la démontrer?
Quand on y réfléchit, c’est simple ! La réciproque se démontre avec le théorème direct ! Si si! Et d’ailleurs c’est sans doute naturellement que les élèves le font sur les cas qu’on leurs propose.
On essaie ?
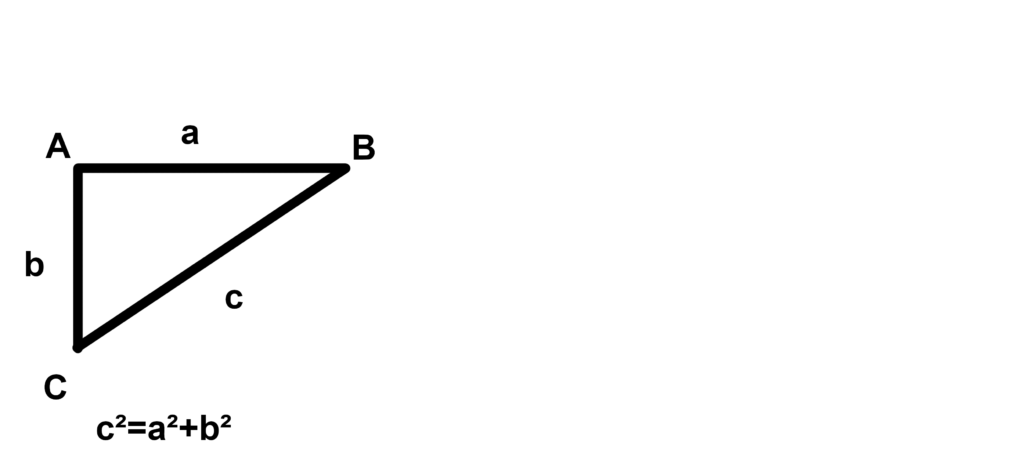
On démarre donc par un triangle ABC , qui vérifie l’égalité de Pythagore.
On va créer un autre triangle A’B’C’, cette fois-ci rectangle, qui possède 2 côtés de même longueur que le premier triangle. On sélectionne les côtés les plus petits.
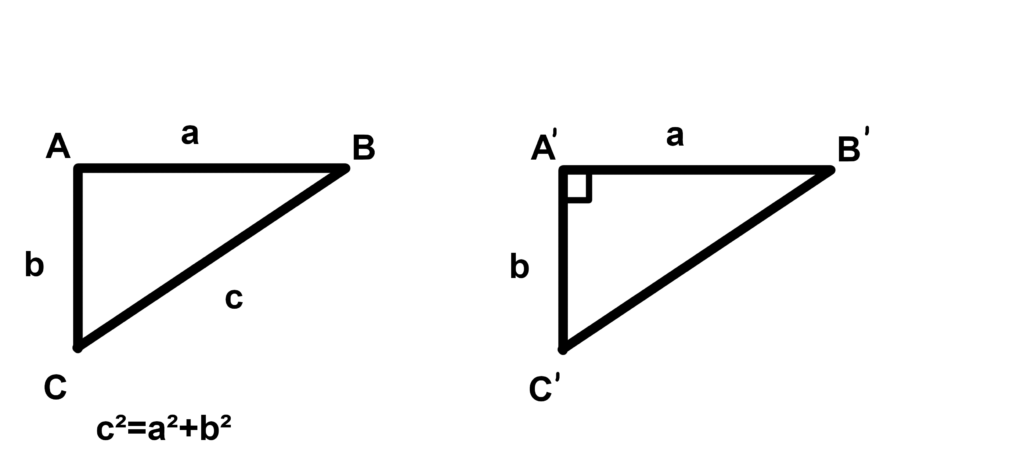
Comme le triangle A’B’C’ est rectangle, je peux donc appliquer le théorème de Pythagore.
J’obtiens donc B’C’²=a²+b², d’où B’C’²=c². Comme B’C’ est une longueur positive, B’C’=c.
On vient donc de montrer que les triangle A’B’C’ et ABC sont égaux, en effet ils ont leurs côtés égaux deux à deux.
Comme ce sont des triangles égaux, ils possèdent également des angles deux à deux égaux, donc ABC est rectangle.
Voilà donc en utilisant les propriétés des triangles égaux, on peut « démontrer » la réciproque du théorème de Pythagore avec le théorème de Pythagore.
Revenons sur un exemple de rédaction élève « mauvaise »
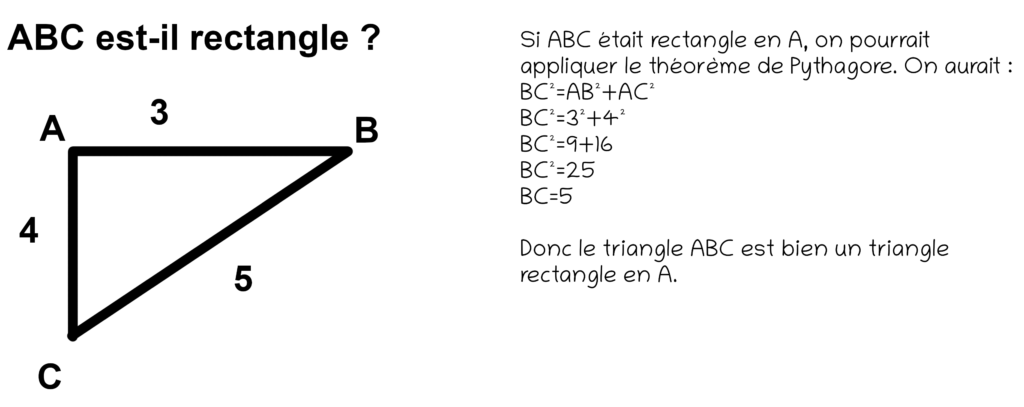
Sur cette démonstration, on peut comprendre que l’élève sous-entend maladroitement l’utilisation des triangles égaux, en testant si on obtient les 3 mêmes côtés.
Donc ici, il n’y aurait pas de problème de raisonnement, sans doute un problème de communication car il ne préciserait pas qu’il utilise la propriété des triangles égaux.
Que faire de ça? Et bien je ne sais pas trop, le mot doit être évoqué, est-ce logique? Parle-t-on de réciproque du théorème de Pythagore au lycée ?


Bonsoir.
Bien vu mais je ne suis pas certain que l’élève ait penser ainsi. Le mieux serait de le tester à l’oral.
Qu’en est-il de la preuve du théorème de Pythagore lui-même ?
et bien ça fera l’objet d’une vidéo donc je ne vais pas spoiler 😀
Patience, patience… As-tu regardé ce que cela donne pour « l’affreuse » réciproque du théorème de Thalès ?
Oui et on n’est pas loin de la réciproque du th de Pythagore mais le passage des triangles semblables reste moins évident et donc c’est facile de parler de réciproque du théorème de Thalès.
Sauf que la rédaction « mauvaise » est extrêmement rare… Je crois l’avoir comptée juste les rares fois où je l’ai rencontré.
Le problème est pour tous les élèves qui n’écrivent pas la supposition « Si ABC était rectangle, on pourrait utiliser le théorème… », ce qui rend toute la suite fausse!
Et pour ceux là, réciproque ou pas réciproque, pas sûr que ça change grand chose.
bonjour j ai une question comment faire pour savoir si un objet est en or pour votre video sur les louis par exemple merci
si vous avez pas compris la question esiter pas a me la redemander
Depuis 2 ans, je mène la séquence sur le théorème de Pythagore en commençant par la réciproque et je trouve que cela a beaucoup plus de sens pour les élèves.
Je n’ai (presque) plus ce problème de rédaction entre le théorème direct et sa réciproque.
Par contre, évidemment, il resterait à se poser la question de la démonstration que je ne traite pas avec les élèves (oui, je sais c’est pas bien, mais bon… si on veut finir les programmes… et promis, je démontre plein d’autres choses…)
Pour ma part, je trouve que la « mauvaise » rédaction n’est pas si mauvaise que cela même sans évoquer les cas d’égalité des triangles…
Sinon que penser des exercices de construction de triangles, devrions-nous aussi demander aux élèves de démontrer que leur construction est « égale » au triangle demandé ?
Nous passons sous silence en permanence les cas d’égalité ou de similitude des figures tracées, ce que les élèves les plus en difficulté ne font pas (hier encore, une élève est venue me montrer son dessin pour que je le valide, vu que dans ma correction, mes points n’étaient pas placé « pareils » !).
Et quand l’égalité n’est pas vérifiée, parlez vous de contraposee du théorème de Pythagore ?
Si on veut être rigoureux sur le vocabulaire (ce que j’essaie de faire et je me bats continuellement entre chiffre et nombre avec eux ) faudrait-il insérer ce mot là ?
Et bien, on peut avec un « si le triangle était rectangle, d’après le théorème de Pythagore, on aurait … or …. donc il n’est pas rectangle »
C’est le raisonnement par l’absurde…
Donc le mot contraposée n’est pas du tout obligatoire.
Le post commence à dater, mais c’est LA question qui m’intéresse en ce moment : j’observe cette année un peu plus de « mauvaise » rédaction chez quelques élèves. Rédaction encore plus problématique que celle présentée plus haut, car ceux-ci ne conjuguent pas au conditionnel mais écrivent « si le triangle est rectangle, alors etc ». Pour prouver que le triangle est rectangle, la formulation de leur raisonnement est plus que maladroite …
Je les reprends car ça ne me permet pas de savoir si le principe est clair pour eux : problème de logique ou de com’ ? Saisissent-ils bien la distinction entre propriété et propriété réciproque ? Seront-ils en difficulté quand il s’agira de propriétés sans réciproques vraies ?
Ca me semble important que ces bases soient claires, dans leur formation de citoyen doué de logique et dans leur parcours scolaire de lycéen par exemple.
Et malgré tout, ce type de rédaction tient la route (avec conditionnel et réf à des triangles égaux), alors je me demande à quel point ça flouterait/éclaircirait leur compréhension en l’évoquant.