Rah, mes 6emes, avant chaque début d’année, je me demande toujours pourquoi, j’ai choisi ce niveau!! Et ensuite, vient la période d’acclimatation (cette période où les élèves doivent comprendre ce qu’on attend d’eux et c’est hyper énergivore!), puis après c’est bigrement rigolo. Pleins de défis sur les représentations parfois fausses qu’ils ont des mathématiques.
Bref, là, j’ai eu plusieurs blocages sur le tracé de parallèle passant par un point, tous quasiment savaient qu’il fallait une équerre et une règle, mais par contre comment tout ça s’agençait : oula oula bof bof! On met la règle en premier, l’équerre à l’arrache sur le point….
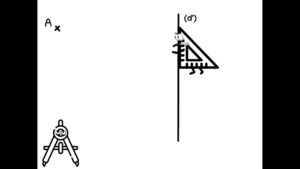Bref, j’ai répété le processus de construction, fait des exemples, mais j’ai toujours eu des blocages jusqu’à ce que je raconte une petite histoire, celle de l’équerre qui voulait déplacer une droite jusqu’à un certain point et… là quand j’ai terminé mon histoire, les réflexions à chaud des élèves (toujours épatés de leurs spontanéités) :
« Ouah , bah là on comprend m’sieur! Avant, c’était fouilli! »
« Trop bien! » « C’est marrant » ..
Et je leur ai dit que j’en ferai une vidéo.
Chose promise, chose due!
Bref, l’avantage des histoires comme avec les nombres relatifs, c’est qu’on créé une image mentale plus solide, liée à des détails et surtout parce que c’est marrant les histoires!
Bon visionnage!
<iframe allowfullscreen="true" style="border:none;width:480px;height:480px" src="https://mathix.org/video/problemes_ouverts/integrateur/index.php?url=https://mathix.org/video/cours/tracer_parallele/tracer_une_parallele.mp4" />
Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :
mais jusqu’aux tables de 5 tout court.
