C’était un objectif que nous nous étions efforcé de valider lorsque nous avons créé les problèmes DUDU avec mon frangin. C’est à partir de ce point de départ que notre réflexion a évolué. Nous avons alors parlé d’intérêt, de curiosité, de « pourquoi? », de « à quoi ça sert? ». Nous n’avons pas réellement franchi la « théorisation » (sortons les grands mooooots!!) de notre démarche.
Sans doute, par ce que nous considérons toujours cela comme une innovation ; un « truc » dont on n’est pas certain que ça marche, qui est perfectible et qui est amené à évoluer. Le doute est toujours présent et on essuie encore parfois des échecs lors de mise en place avec certaines vidéos.
Je me rappelle que tout récemment, j’ai tenté le problème DUDU sur le dentifrice. J’avais fait un sevrage de mes élèves sur le problèmes DUDU, je souhaitais savoir au bout de combien de temps ils me les demanderaient. 5 semaines, 5 semaines ont suffit et des élèves m’ont demandé timidement : « heu, m’sieur, on pourrait pas faire des DUDU?« .
Me rappelant que Julien m’avait dit quelques temps avant : « Le problème sur le dentifrice en fait c’est une tuerie! Ça soulève des débats intéressants, j’ai adoré …« . C’est donc sans sourciller que j’ai proposé ce problème.
La douche froide. Les élèves sont entrés dans l’activité, ont su repérer le soucis, mais le passage à l’écrit a été très difficile. « Que mettre? » « Pourquoi? » « En fait, c’est évident » « Pfff c’est nase, non? » (c’est en gros le cheminement des réflexions qu’ont suivi les élèves). Jusqu’à ce qu’un courageux ose : « M’sieur, on pourrait pas en faire un autre?« .
Méga douche froide! Bref, j’ai refusé en disant qu’on abandonnait pas face à la moindre difficulté et j’ai, par conséquent, par ce refus, forcé la mise au travail. Les élèves ont fait le travail, pas avec un engouement extraordinaire, les productions sont d’ailleurs très moyennes.
Je me suis donc vu refaire une autre séance problème DUDU ( sur les canettes de Coca-Cola) qui, elle , a très bien marché, ouf! Et spécial dédicace à la 4eA! 😉
Pourquoi je parle de cela?
J’ai fait récemment une formation sur les EPI-maths-Techno qui a dévié vers la démarche de projet (d’ailleurs repris par une autre formation sur la démarche de projet… avec Cédric Le-Goff, malheureusement un peu double emploi mais tout aussi intéressant).
Jean-Paul Clad, le formateur, a expliqué ce qu’il faisait et a mis des mots sur sa démarche.
Il a parlé d’activité déclenchante, processus d’apprentissage/formation et processus de création/production.
- Pour initier une démarche active d’apprentissage par les élèves, il faut donc une activité déclenchante efficace, qui permette à l’élève d’entrer dans une activité mathématique. En gros, il doit faire des maths de manière volontaire. Cette activité est donc primordiale pour avoir des efforts efficaces de la part de l’élève. Il deviendra acteur.
- Une fois cela fait, on est dans le processus de résolution du problème, et attention ! On doit naviguer entre deux eaux :
- D’une part, le processus d’apprentissage, en gros on doit sortir légèrement l’élève de sa zone de confort, pour qu’il entre dans ce qu’on appelle la zone d’apprentissage. C’est à partir de ce moment que l’élève apprendra. Cependant, en sortant de sa zone de confort, l’élève peut, par contre, avoir une chute dans la motivation.
- D’autre part, le processus de création, en gros l’élève, ici a le plus de liberté pour restituer sa réponse, il devient donc pleinement acteur et maître de sa démarche. C’est ici, que l’élève retrouve sa motivation. Il est donc important que le projet se termine pour « satisfaire » l’élève.Cependant dans cette phase du fait de sa liberté il revient naturellement dans sa zone de confort (il n’apprend plus).
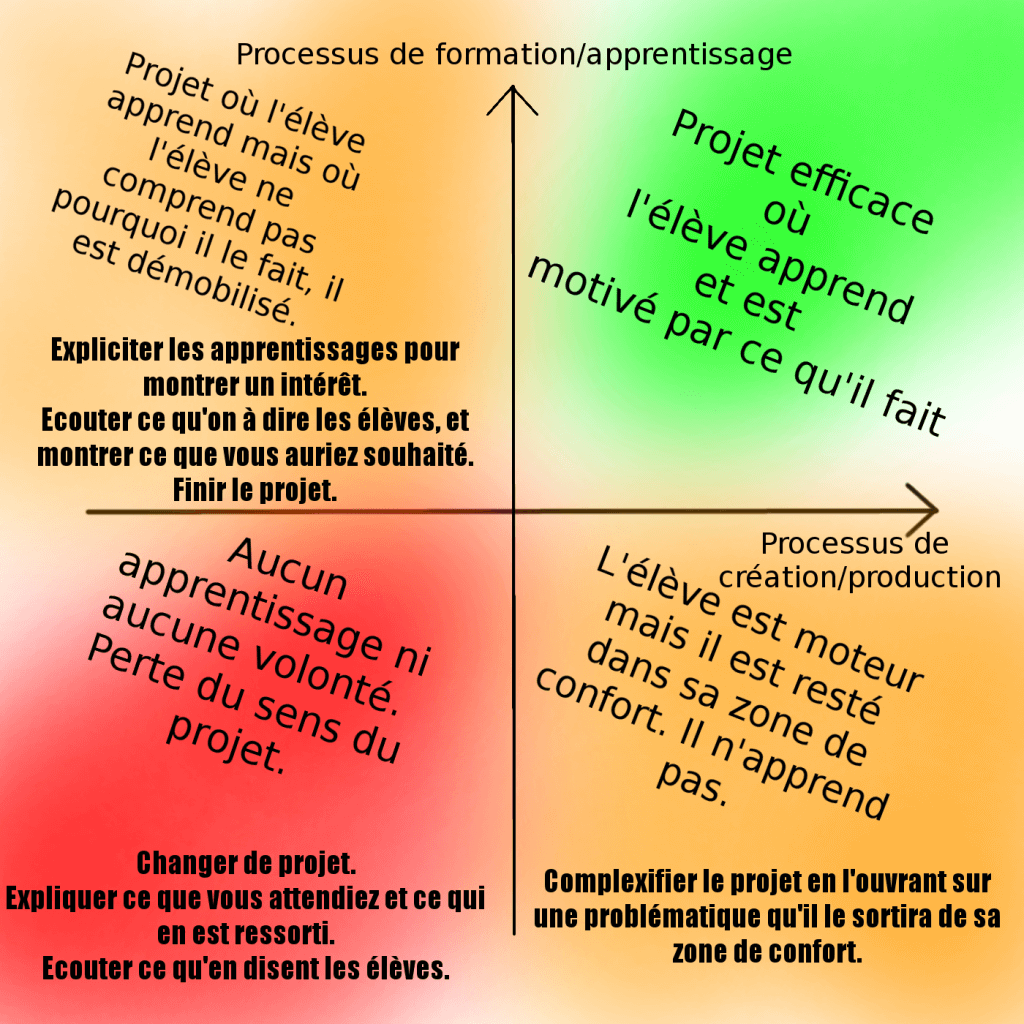
On peut résumer cela dans un graphique que j’ai fait (à améliorer sans doute) :
Après, dans l’absolu, pour tous les projets menés, tous n’ont pas réagi de la même manière, certains sont resté dans leur zone de confort, d’autres ont appris. Je pense qu’il est difficile d’avoir un projet efficace (motivant et qui permette d’apprendre) pour tous.
Voilà, bref, plutôt content d’avoir mis quelques mots
sur des démarches approchantes que j’avais. 🙂