Ouh lala, le titre est osé, mais tant pis, il illustre une discussion que j’ai eu avec Julien sur le théorème de Pythagore d’abord puis on a dévié sur le théorème de Thalès et c’est une réflexion que j’ai pu avoir certains de mes collègues …
Alors cet article n’a pour but que de poser un questionnement et non faire de la provocation, l’idée est claire dans mon esprit. C’est une vraie gêne que j’ai vis-à-vis du programme du cycle 4 tel qu’il est annoncé et je n’ai pas vraiment de solution satisfaisante.
I.Le théorème de Pythagore
Alors j’en avais déjà parlé là, d’ailleurs dans cet article, je montre la démonstration de la « réciproque du théorème de Pythagore » (je vous laisserai la voir,en plus elle fait l’objet d’un projet de preuve par DU²), cette démonstration repose sur le théorème de Pythagore direct et les triangles égaux.
Cela pose question surtout qu’en mathématiques pour tout le reste, on aura tendance à utiliser le mot réciproque surtout lorsque la démonstration ne découle pas du premier, autrement on parle directement d’équivalence.Or là, la réciprocité de ce théorème repose sur les triangles égaux, c’est évident pour les élèves et également des professeurs.
Souvent les élèves ont tendant à (re)calculer un côté et conclure en fonction de ce qu’il trouve, en fait ils utilisent les triangles égaux de manière implicite. ( notion vue 5e)
D’ailleurs au brevet, nous ne pénalisons pas les élèves pour ne pas faire la différence entre réciproque et théorème, je peux me poser la question si ce n’est pas pour cette raison.
En fait, le théorème de Pythagore se suffit amplement à lui-même et permet rapidement de démontrer qu’un triangle est rectangle ou non.
Peut-on parler de simplification de rédaction? Non car parfois les élèves ne savaient pas quoi choisir, contraposé, réciproque, sens direct avec une rédaction très figée. Alors que pour montrer qu’un triangle n’est pas rectangle, le théorème de Pythagore le peut, pour montrer qu’un triangle est rectangle, le théorème de Pythagore le peut aussi, pourquoi s’embarrasser d’une réciproque… qui ne sert à rien?
On pourrait arguer à juste titre que les élèves doivent travailler la notion d’implication, de réciproque, d’équivalence.
Sauf que comme je l’ai dit, on peut démontrer qu’un triangle est rectangle ou non en utilisant simplement le théorème de Pythagore.
Alors pourquoi ne pas transformer le théorème de Pythagore en une équivalence avec un « si et seulement si » et de démontrer le sens direct et réciproque rapidement? Ça simplifierait bien des tracas et surtout une égalité de traitement entre les professeurs qui vont accepter et ceux qui vont refuser.
Et puis…. cette notion de réciproque pose problème surtout avec le théorème de Thalès.
Les deux mots réciproques dans « réciproque du théorème de Pythagore » et « réciproque du théorème de Thalès », n’ont pas le même sens !
II.Le théorème de Thalès
Normalement si on a une propriété avec deux propositions P et Q : P→Q alors la réciproque est Q→P.(d’ailleurs elle fonctionne bien pour le théorème de Pythagore).
Entendons-nous, une réciproque d’un théorème existe toujours, elle est, dans certain cas, vraie, dans d’autres cas, fausse.
D’ailleurs la réciproque d’une implication fausse peut être vraie. Et si la réciproque d’une implication vraie est vraie, on parle d’équivalence.
Donc effectivement si on s’en tient à cette définition, le théorème de Thalès tel qu’il est écrit a bien une réciproque mais… pas celle-là.
Jouons à un jeu.
Le théorème de Thalès (avec l’utilisation des triangles semblables, la forme est plus simple et cohérente avec ce qu’on pourrait enseigner en 4e, au pire on dira que les longueurs des côtés entre les triangles sont proportionnelles, mais c’est long à écrire.) :
« Soient deux droites sécantes coupées par deux autres droites. Si ces dernières sont parallèles alors les deux triangles ainsi formés sont semblables. »
La réciproque de cette affirmation devient :
« Soient deux droites sécantes coupées par deux autres droites. Si les deux triangles ainsi formés sont semblables alors ces dernières sont parallèles. »
Un simple contre-exemple suffit pour montrer que cette proposition est fausse.
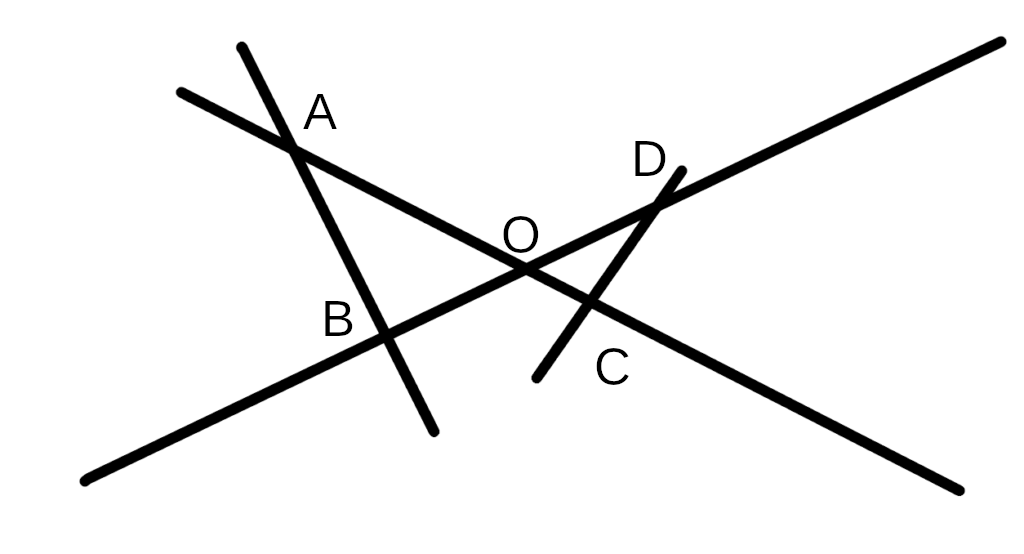
Donc logiquement je suis en droit d’affirmer que la réciproque du théorème de Thalès n’est pas vraie.
On le sait, il y a plus et moins de conditions pour obtenir le parallélisme de deux droites.
Le moins, deux rapports égaux au lieu de trois.
Le plus, un ordre précis des points de concours.
En fait, on cherche à montrer que les triangles sont homothétiques l’un de l’autre, on va montrer que C, D et O sont l’image par une homothétie de centre O respectivement de A, B et O. Pour le point O c’est trivial donc on se limite à 2 points donc deux rapports.
Dans le rapport homothétique, le sens a une importance d’où l’ordre des points, on veut éviter ce cas-là (bien connu puisque très classique)
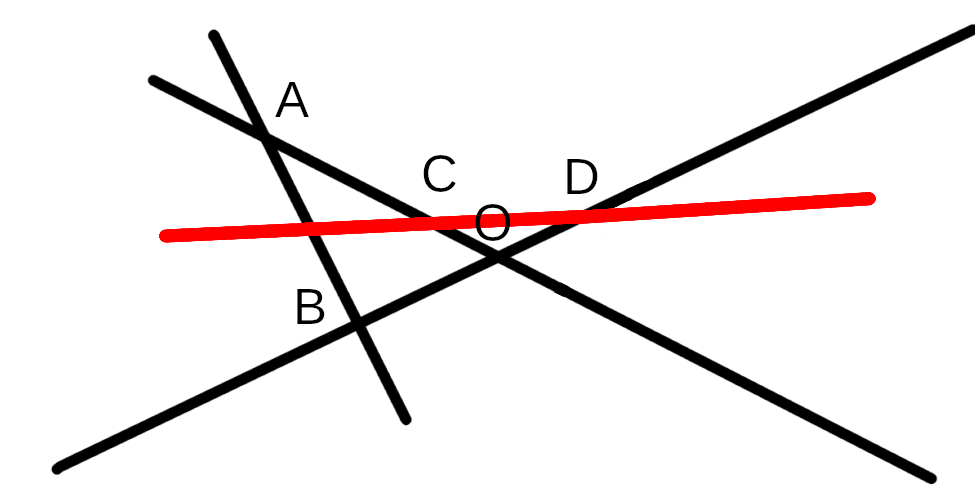
On se retrouve donc bien avec ce type de figure lorsqu’on est dans le cas d’une homothétie. :
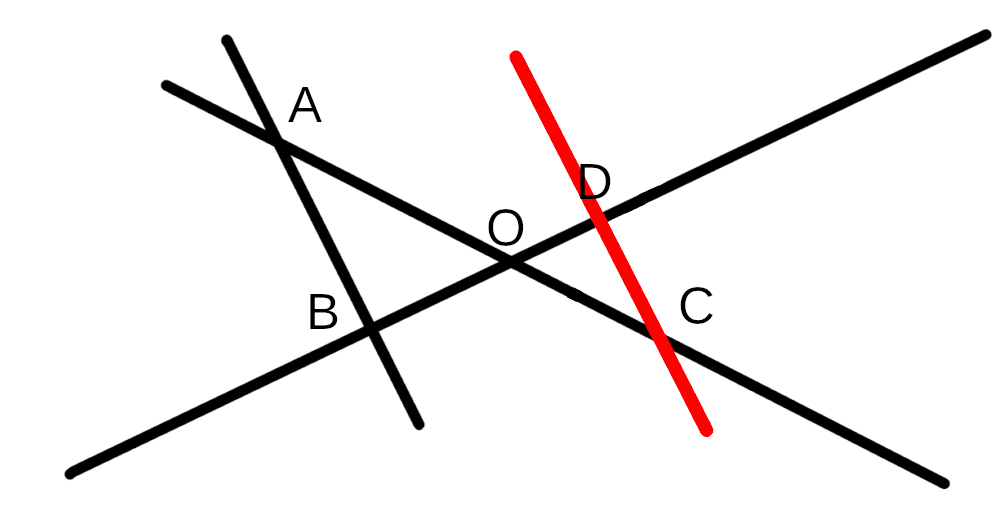
donc cela pose question sur l’intitulé du théorème de Thalès lui-même tel qu’on l’enseigne en 4e et 3e.
Reprenons donc cet intitulé pour que la réciproque du théorème de Thalès soit cette fois-ci vraie.
Je propose :
« Soit deux droites sécantes coupées par deux autres droites,si ces dernières sont parallèles alors les deux triangles ainsi formés sont homothétiques. »
On ne perd rien sur le théorème direct, on a juste une précision sur la disposition des triangles l’un par rapport à l’autre.
Dans ce cas , la réciproque est vraie et les conditions sont tout à fait valables.
MAIS (il faut bien un mais) la notion d’homothétie est privilégiée en 3e (voir les repères de progressivité).
Donc que faire?
Doit-on apprendre un demi-théorème de Thalès en 4e (ce qui est déjà le cas d’ailleurs car on se limite au cas des triangles emboîtés) que l’on reformule ensuite en 3e?
J’en viendrai presque à me dire pour couper la poire en deux qu’on doit parler de triangles semblables en 4e et de parler du théorème de Thalès avec le mot semblables et d’évoquer la l’homothétie en 3e et de revenir sur la proposition du théorème de Thalès en disant qu’on perd une information cruciale, les triangles sont, en fait, homothétiques.
Quoi qu’il arrive, il faudrait déjà considérer le théorème de Thalès comme rapport entre deux triangles et non une simple égalité de rapports, car on perd la notion de transformation sous-jacente.
Bref ces points sur le théorème de Pythagore celui de Thalès m’amène à penser que la notion de réciproque est quand même très malmenée, rendu inutile dans un cas et fausse dans l’autre…
Doit-on continuer à galvauder la notion de réciproque? A quelle fin?


Il y en a qui sont forts pour se compliquer la vie… Le théorème de Pythagore est une équivalence entre l’angle droit du triangle et l’égalité. On peut bien parler de réciproque, ça ne sert pas grand-chose ! Le théorème sert à calculer la longueur d’un côté ou monter qu’un triangle est rectangle (ou pas), mais c’est toujours le même théorème, pas besoin de parler de réciproque. D’ailleurs, en Suisse, ce mot n’apparaît pas quasiment pas dans les manuels, et sûrement pas pour Pythagore.
Mdr vous êtes tellement forts à ne pas chercher à comprendre. Allez jetez un coup d’oeil sur l’analyse fonctionnelle où on l’on parle de produit scalaire et des espaces normés , c’est là que vous allez comprendre d’où vient ce théorème
C’est un propos réducteur et le théorème de Pythagore a bien été inventé sans la notion de produits scalaires ou espace normé, de là à en croire qu’il est issu de ça, c’est plutôt l’inverse,le théorème de Pythagore Pythagore a permis de créer une norme et pas l’inverse.
Ton propos est quand même hors sujet, je parle d’enseignement des maths, hein! 😉
Bonsoir et merci pour cet article.
Néanmoins, sachez que la réciproque de Thalès est présentée à mes élèves comme étant fausse. Preuve à l’appui, les figures pathologiques que je fais étudier à mes élèves lors d’une première activité.
En deuxième activité, les élèves trouvent eux même la condition à ajouter pour que la réciproque devienne vraie. Franchement, après avoir précisé cela, je ne trouve pas scandaleux de présenter le résultat de leurs recherches sous le titre de réciproque de Monsieur Thalès.
Bien à vous !
A modifier les conditions, la propriété devient vraie mais ce n’est plus la réciproque du théorème de Thalès (ce n’est plus rigoureusement la réciproque en inversant conditions et conclusion), c’est en cela que l’on se trompe.
Comment se compliquer la vie pour rien. Pourquoi vouloir reformuler le th de thales à la sauce triangles semblables ou homothetiques? Vousle dites vous même ca vous pose des problèmes… Gardons le theoreme comme il est écrit avec des rapports de longueurs comme on l a enseigné depuis des années. Pour la » réciproque » on precise l ordre des points et basta. Introduire les triangles égaux et semblables et essayer de tout démontrer avec est un non sens quand on a supprimé la moitié du programme de géometrie au college. Si déjà les eleves sont capables d utiliser un theoreme et sa reciproque ce sera pas mal! Pour ma part j utilise l ancienne version et je precise que la reciproque de thales est fausse sauf si on ajoute l ordre des points, par abus de langage on continue a dire reciproque de thales et plus de problemes. Sachant qu on peut faire une equivalence si on raisonne en termes de mesures algebriques, on peut trés bien dire que ce sera vu plus tard. Les eleves n ont plus les moyens de raisonner correctement en geometrie, ce genre de debat aurait un sens si ils maitrisaient la logique de base mais là je trouve qu on met la charrue avant les boeufs. Faisons simple, sens direct reciproque contraposee c est deja pas mal au collège d arriver à maitriser cela..
Très intéressant comme débat mais guère innovant, pédagogiquement parlant. Je vous propose un autre sujet. Alice et Noé vont au restaurant, ils paient le même prix le repas Alice avait 80€ et Noé 65€. Le rapport du reste d’argent d’Alice sur le reste de Noé est de 7/4. Combien ont-ils payé ? Évidemment pour des
4ème je proposerai la methode visuelle de Singapour. Nous sommes ici dans la lecture de proportionnalité… Il s’agit bien de pédagogie des maths. C’est d’une heuristique qu’il s’agit. La methode classique algébrique venant après. Merciiiiiiiiii
– Concernant Pythagore, l’ancien programme ne distinguait pas le théorème de Thalès de sa réciproque, me semble-t-il. Et maintenant, on le fait …
– Concernant Thalès, je dis à mes élèves que ce n’est pas exactement la réciproque tu théorème de Thalès qui est énoncée car effectivement, la vraie réciproque du théorème de Thalès est fausse (on peut même écrire avec des guillemets « réciproque » du théorème de Thalès). On a renforcé une des conditions pour que cette « réciproque » devienne vraie.
– Et si cela embête vraiment un prof très rigoureux d’avoir une fausse réciproque du théorème de Thalès, pourquoi ne pas énoncer le théorème de Thalès en remplaçant la condition des deux droites sécantes par la condition de l’alignement des points dans le même ordre. Et alors, la bonne réciproque du théorème de Thalès devient vraie !!!
Je voudrais vous parler de Thalès (théorème, réciproque et contraposée) et surtout d’échanger avec vous sur vos pratiques. C’est un chapitre qui est particulier pour trois raisons.
– La première est que le théorème de Thalès peut s’énoncer de plusieurs façons différentes. Une des deux hypothèses (la moins importante) est d’avoir soit deux droites sécantes « les droites (AM) et (BN) sécantes en O », soit des points alignés « O, A, M et O, B, N alignés », soit deux points qui appartiennent à deux droites différentes « A appartient à (OM) et B appartient à (ON) ».
– La deuxième est que la réciproque n’en est pas exactement une. En effet, l’hypothèse précédente est insuffisante et doit obligatoirement être remplacée par une hypothèse plus contraignante à savoir « O, A, M et O, B, N sont alignés dans le même ordre ».
– La troisième est que dans la réciproque, on n’a pas besoin de comparer les 3 rapports de longueurs alors qu’ils apparaissent tous les 3 dans la conclusion du théorème de Thalès. Pour ce qui est de la réciproque (qui sert à démontrer que deux droites sont parallèles (AB) et (MN) par exemple), il faut obligatoirement comparer les deux rapports de longueurs issues du sommet commun O (ie OA/OM et OB/ON dans mon exemple). Pas question de prendre AB/MN.
Dans notre collège, on a décidé de prendre parmi les hypothèses du théorème de Thalès la formulation des droites sécantes ; ceci afin d’avoir une uniformisation de la rédaction lors des devoirs communs et des DNB blancs.
Maintenant que j’ai posé les bases de la discussion, je voulais surtout parler de la contraposée du théorème de Thalès : si OA/OM n’est pas égal à OB/ON alors les droites (AB) et (MN) ne sont pas parallèles. Dans la rédaction, certains utilisent le mot contraposée et écrivent « d’après la contraposée du théorème de Thalès ». Idem d’ailleurs avec Pythagore. D’autres se contentent d’écrire « puisque que OA/OM n’est pas égal à OB/ON, on en déduit que les droites (AB) et (MN) ne sont pas parallèles ». J’ai même vu aussi « d’après la conséquence du théorème de Thalès ».
Quelques questions concernant cette contraposée :
1) Quand OA/OM n’est pas égal à OB/ON, faut-il parler en plus d’une hypothèse supplémentaire qui permet de visualiser une configuration de Thalès (triangles emboîtés ou version papillon) ? Si oui, deux questions méritent qu’on s’y attarde :
1) doit-on parler de l’hypothèse mise dans le théorème de Thalès (voir celle retenue plus haut) ou bien de celle de la réciproque (O, A, M et O, B, N sont alignés dans le même ordre) ? On pourrait penser plutôt à l’hypothèse du théorème de Thalès (droites sécantes dans notre collège) vu que cette contraposée est une conséquence directe du théorème de Thalès. Mais alors que faire quand on a une question ouverte du type : les droites (AB) et (MN) sont-elles parallèles ? On ne sait pas alors si on utilisera la réciproque ou la contraposée …
2) par ailleurs, est-il préférable d’écrire d’abord cette hypothèse puis de comparer ensuite les rapports de longueurs ou de faire l’inverse ? Cela peut paraitre futile mais ce n’est pas certain.
En fait, cela dépend déjà comment vous organisez votre chapitre.
– soit vous faites théorème puis réciproque puis contraposée ;
– soit vous faites théorème puis contraposée puis théorème.
Dans la première organisation, alors le pb ne se pose plus. Que l’on ait (ou pas) l’égalité (et donc qu’on utilise la réci ou la contraposée), je conçois qu’on puisse parler dans les deux cas de la condition des points alignés dans le même ordre. Et peut importe ici si on fait la comparaison en premier ou en second.
Par contre, dans la seconde organisation, alors je vois mal écrire « points alignés dans le même ordre » comme hypothèse de la contraposée. Et avec cette progression, si la question est ouverte (les droites sont-elles parallèles ?) alors on est obligé d’abord de comparer les rapports de longueurs (les bons) puis de parler de points alignés dans le même ordre (si on a l’égalité) ou de parler ensuite de l’hypothèse du thm (si on n’a pas l’égalité).
Néanmoins comme la contraposée est la conséquence immédiate du thm de Thalès, il peut paraître plus naturel de faire d’abord contraposée puis réci.
Je me pose toutes ces questions car je faisais jusqu’à présent thm puis réci puis contraposée. Mais cette année, je voudrais inverser la réci et la contraposée dans ma progression. D’où mes interrogations.
Désolé de ne pas avoir pu répondre à ton mail, manque de temps, mais promis j’essaie de te répondre dès que je trouve un peu de temps à consacrer à ça.