Bonjour à tous!
Bon bah je profite de mes après-midi de récupération pour potasser des notions et surtout les notions de 6emes, je me sens toujours un peu à la ramasse, je pense que parfois j’ai du mal à cerner les enjeux comme il faut. La vraie claque avait été la formation de Bruno ROZANES et Stéphanie EVESQUE sur les nombres décimaux. D’ailleurs là je revois la progression de 6eme complètement et j’essaie de convaincre mes collègues de faire de même (car on fonctionne en progression commune pour tous les niveaux).
Et je continue mon train-train sur les 6emes. Un niveau que je n’aime pas beaucoup car il me sort totalement de ma zone de confort, là où les enjeux d’autonomie, de prise d’informations, de critique, de prise de recul sont évidents pour moi et la progression didactique des notions mathématiques est évidente pour moi dans la construction du cycle 4, c’est plus nébuleux en cycle 3.
Déjà j’ai contacté l’école de mes enfants pour un stage d’observation voir de la co-animation avec la collègue qui gère le CM1 et CM2 ce qu’elle a accepté. (YES!)
Puis là, mon regard s’est posé sur le fameux calcul de proportion.
3/4 de 6 c’est quoi ? Comment on le construit?
Je partage donc 6 en 4 et je prends 3 parts. Donc l’opération devient 6÷4×3. ok
Mais comment venir au « raccourci » 3/4 de 6 c’est aussi 3/4×6 ?
Généralement je passais au côté algébrique.
1/4×6 = 6/4 et 6/4=6÷4 car 6/4 c’est le nombre qui multiplié par 4 donne 6 et ce nombre dans cette multiplication à trou peut se trouver en procédant à l’opération contraire, la division.
Bon c’est un chemin alambiqué, pas toujours à l’aise avec ça.
L’idée reste de convaincre et parfois une démonstration rend encore plus confus les choses, même si certains s’en accommodent , les élèves en difficulté peuvent être perdus.
Bref, j’ai voulu rendre ça visuel à partir de carrés unités.
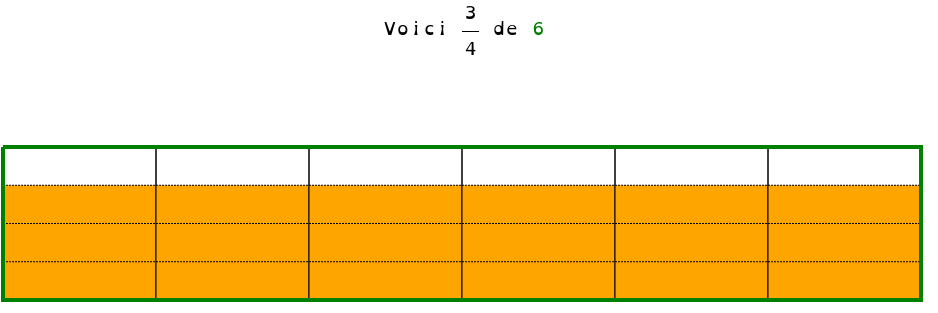
devient

Alors, je m’interroge encore, mais je pense le tester en 6eme. C’est en testant qu’on voit si ça marche …
Voilà l’application qui permet de générer l’animation :


Bonjour,
Peut-être que tu peux rajouter au début le rectangle qui représente l’unité ? Sinon, c’est top.
Laurent
merci c’est génial
Salut Arnaud!
Merci pour le partage de tes réflexions… Ma vie de profs de maths ne me permet pas toujours de collaborer à hauteur de mon inspiration, mais aujourd’hui, je prends le temps. En espérant que cela n’en reste pas là… Tu as désormais mon adresse mail « privée permanente » (4 ans @ac-nice.fr, 3 ans @lfo.no, et encore indéterminée @efb.rs).
J’aurais privilégié une première approche préalable:
1. Comment peut-on représenter le nombre 6?
Réponses possibles: une longueur; une aire (6 carrés unitaires [c’est ton rectangle à fractionner aux 3/4]; un disque; etc.); un volume (mais là, en 6e ou avant ou après, les élèves se rendront assez vite compte que la « modélisation » d’un volume unitaire pourra être un verre rempli d’eau et que pour l’exploitation du fractionnement, il sera « préférable » ou « plus facile » que le verre soit un cylindre, ce qui ramènera le problème à revenir à une aire, et que là, l’aire unitaire sera un rectangle, vue en coupe du verre, donc cela rentre dans le « etc. » de la parenthèse de « une aire »).
1.1 Si on prend le disque, alors la visualisation des 3/4 du disque passe bien par le fractionnement en 4, chaque partie étant 1/4. Donc l’approche privilégie ton 3/4 x 6 passant par 1/4 x 6, c’est à dire le recours au langage naturel « un quart » ou « un quart de » pour pratiquer à nouveau la numération « 1 quart, 2 quarts, etc. ». Cela permet aussi de repenser le sens de numérateur et dénominateur: dénominateur « dénomme » le mode de partage équitable ici en 4 parties, et numérateur « énumère » ou « numérote par cumul ».
1.2. Le rectangle. Là, contrairement au cercle, on n’a pas « une infinité de diamètres », donc de façon de couper d’abord en 2…
2. Combien le rectangle a-t-il d’axes de symétries?
2.1 Si on partage selon les deux médianes: à un coefficient de perspective près, on retrouve la même approche que pour le cercle, ou un carré découpé en 4 petits carrés.
2.2 Si on coupe en 4 selon la direction de la médiane de la largeur (puis chaque demi-largeur par médiatrice), on retrouve ton 3/4 x 6 et le 1/4 x 6 est une bande horizontale. C’est comme si on prenait pour chaque verre 3/4 de son contenu: 3/4 x 1. Donc par cumul 3/4 x 6.
2.3 Si on coupe en 4 selon la direction de la médiane de la longueur (puis […] idem), on va d’abord prendre 1/2 x 6 à gauche et 1/2 x 6 à droite. Donc obtenir 1/4 x 6 gg et 1/4 x 6 gd et 1/4 x 6 dg et 1/4 x 6 dd. Dans ce cas, cela revient à « oublier » que l’on a 6 verres séparés et les cumuler dans parallélépipède rectangle, que l’on va pouvoir partager globalement en le fractionnement qui nous arrange. Et là, justement, ce n’est plus le partage de la numération 1,2,3,4,5,6 verres mais 1,2,3,4 quarts du total.
Ma conclusion: ta démarche et la mienne « plus large » (sans lui donner de prépondérance en importance) sont toutes les deux intéressantes. Mais elles se fondent sur un principe qui selon moi prime et de loin:
4 x 1/4=1
4 x [qqch]/4 = [mon qqch]
Et c’est à partir de là qu’on « revient en arrière »: au lieu d’en prendre 4, on en prend autant qu’on veut!
Et tout d’abord moins que 4. par exemple 3.
Puis en supposant que la ressource puisse être fournie en plus grande abondance: 5, 6, 7, etc.
D’où le passage d’une proportion à un fraction non proportion.
Et c’est plus tard que la définition: 3/7 est le nombre qui multiplié par 7 donne 3 prendra son sens…
Au plaisir de lire ta réaction.
Pardon si mes écrits paraissent présomptueux, j’essaie de faire vite et efficace, sans perdre en pertinence et conviction, dans l’intérêt de nos quêtes perpétuelles de l’idéal de la transmission du sens profond des choses…
« quels sont les axes de symétrie du rectangle? »