Catégorie : Réflexions

par Arnaud Durand

L’appropriation d’une notion dans la compétence calculer

Bonjour à tous.

Bon voilà, je vais présenter un peu ma réflexion qui s’appuie en partie des échanges lors de formation et de groupe de réflexion.

La compétence « calculer » est complexe à mettre en œuvre au collège, il faut une base solide d’apprentissage pour acquérir une nouvelle notion et on a parfois tendance à aller vite (moi le premier).

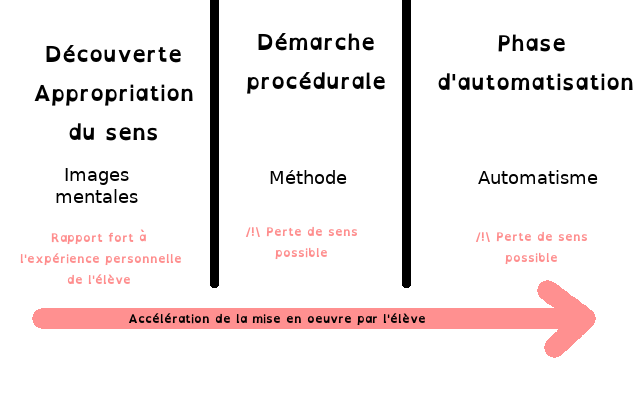
L’acquisition d’une nouvelle notion se fait en 3 phases.

  1. Appropriation du sens et lien avec les notions déjà acquises.
  2. Phase procédurale
  3. Automatisation

Ces 3 phases sont importantes, et on a tendance à négliger ou plutôt passer rapidement sur la première phase, à peine le sens de la notion compris, on file sur la procédure, et là malheureusement peu de lien entre les deux sont faits.

Pour éclairer mon propos, je vais revenir sur la distributivité.

Cette notion est à acquérir au cycle 4 (vocabulaire développer ) et est à voir dès la 6eme au cycle 3 avec les astuces de calcul (distributivité sur des expressions numérique du genre 6 \times 15=6 \times 10+6 \times 5 ).

Généralement, les astuces de calcul sont comprises assez rapidement en 6eme, en revenant au sens de la multiplication, comme répétition de l’addition.

Au cycle 4, l’extension se fait du point de vue littéral et avec également des facteurs non entier. Ici, l’argument de la répétition ne tient plus forcément.

Alors d’autres processus plus ou moins complexes existent pour expliquer ou illustrer la distributivité, ce qu’on appellerait des preuves visuelles (ou aussi des représentations). Pas vraiment rigoureuses, mais suffisantes pour que les élèves comprennent cette notion avec des éléments qui leurs parlent. L’idée étant de faire du lien avec des connaissances personnelles qu’ils possèdent.

Donner une seule illustration de la distributivité n’est donc en soi pas assez suffisant, l’idée est d’en proposer des plurielles, puisque chaque élève a un vécu, des appétences uniques.

J’avais d’ailleurs une vidéo dessus recensant ces images mentales.

Bref, ces images font sens et permettent d’ « expliquer » ce qu’est la distributivité. (même si ici, il n’y a pas de preuve à proprement parler puisque la distributivité est intrinsèque au corps, mais je souhaite me servir de ma vidéo, donc là, on a plus des images mentales et des représentations.)

Enfin de je termine ensuite par une astuce pour développer, c’est ce que j’appelle la « procédure« , ou plutôt la démarche procédurale.

La vidéo :

Ici, le sens se perd un peu plus (les flèches, le facteur qu’on distribue), mais la procédure permet d’alléger la réflexion, de transformer le processus réflexif lié au sens vers un processus mécanique. C’est important car pour aborder un problème mathématique, il faut avoir l’esprit qui ne s’empêtre pas dans la réflexion calculatoire.

Ensuite, vient la phase de l’automatisation, où là l’esprit n’est plus accaparé par le calcul.

On n’a tendance à donner rapidement la procédure sans s’attarder suffisamment sur le sens. Cela génère des erreurs, il faut donc rappeler les images mentales qui font sens pour que l’élève comprenne son erreur. L’intérêt donc des images mentales est de vérifier la cohérence de ce que l’on fait a priori et a posteriori.

C’est un peu comme l’apprentissage des tables de multiplication, des élèves parfois compte sur leurs doigts reprenant le processus itératif de l’addition, ils ont compris la notion de multiplication, mais perdent de l’énergie dans ce processus et ne peuvent ainsi que trop difficilement aborder un problème mathématique.Le fait de connaître les tables permet d’aller plus vite, mais il ne faut pas perdre le sens, ce qui permet de se corriger.

Vous avez parlé du tableau de conversion?

J’aimerai revenir sur un autre écueil qui est celui du fameux tableau de conversion (surtout celui des aires). Cet outil est clivant. Des profs « pour », d’autres « contre », d’autres un peu des deux.

Tiens, j’en ai un pour vous : https://mathix.org/conversion/index.html

Les documents d’accompagnement sont assez explicites dessus, les élèves doivent le voir, mais ce ne doit pas être le canal principal pour expliquer la conversion d’aire (ou même longueur ou quoique ce soit d’autre).

1)On doit reprendre le processus suivant pour convertir 2,4cm² en m² :

A=2,4 cm ^2

Par une petite astuce de calcul

A=2,4 \times 1cm^2

Par définition de l’unité 1cm², c’est l’aire d’un carré de côté 1 cm.

A=2,4 \times 1cm \times 1cm

par définition des grandeurs simples : 1 centimètre est un centième de mètre.

A=2,4 \times 0,01m \times 0,01m

Astuce de calcul

A=2,4 \times 0,01 \times 1m \times 0,01 \times 1m

On réordonne et on calcule, on peut utiliser le glisse nombre pour la multiplication par 0,01 , les unités deviennent des centièmes :

A=0,024 \times 0,01 \times 1m \times 1m

A=0,00024 \times 1m \times 1m

Par définition du m² , c’est l’aire d’un carré de côté 1 m

A=0,00024 \times 1m^2

A=0,00024 m^2

Voilà donc là de manière sensée, on est passé par la notion des grandeurs simples.

2) On pourrait également donner l’image mentale que dans un carré de 1m, il y a 100 carrés de côté 1dm et dans un carré de 1dm, il y a 100 carrés de côté 1cm. Ce qui fait 100 \times 100 carrés de 1cm de côté dans un carré de 1 m de côté, soit 10 000 carrés.

Donc 1 cm² est 1 \over 10000eme de m² et on peut passer à la conversion par le glisse nombre par exemple : « Il faut 10 000 cm² pour faire 1m² donc on divise par 10000, les unités sont 10 000 fois moins fortes »

3) Ou sinon, et bien on adapte l’outil du tableau de conversion, on le construit avec les élèves, et on explique la démarche.

Certes l’outil fait perdre du sens , mais il permet aussi d’aller vite, de pouvoir se concentrer sur le problème mathématique.

Rien n’empêche de faire les deux, pourvu que les élèves puissent se reprendre avec les images mentales fortes des carrés.

De plus cet outil doit être vu et expliqué, les parents d’élèves eux, l’ont vu et ont tendance à l’utiliser. Il faut donc préparer les élèves à des outils qui n’ont pas de sens, et essayer de leur en donner en le construisant avec eux.

Le tableau de conversion a donc pour moi parfaitement sa place au sein des apprentissages et ne doit pas être renié.

À-propos :

Bon c’est une réflexion et mon avis aujourd’hui, rien ne m’empêchera de changer d’avis. Je sais que Claire Lommé, pour en avoir parlé avec elle, fera peut-être une réponse à cette réflexion.

Moi, j’aime bien Claire (je crois que c’est réciproque), on n’est pas tout le temps d’accord, mais on ne s’est jamais méprisé, elle a toujours su rester constructif tout comme j’ai essayé de l’être. Et puis chacun évolue, on a des opinions, et c’est le fait d’échanger qui nous fait évoluer. La critique doit permettre une réflexion et non assouvir du mépris.

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

TEDX : L’art de poser les bonnes questions : la questiologie.

Bonsoir à tous!

blank

Voilà je suis tombé sur cette conférence TedX de Frédéric FALISSE, une belle remise en question (rhô fallait que je la fasse puisque ça parle de questions) sur la manière que l’on a de faire réfléchir nos élèves et également la manière dont on pose des questions.

A voir et revoir.

Télécharger

Pour y réfléchir :

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

Groupe de réflexion sur les classes inversées

J’ai reçu, en fin d’année, un mail de Catherine LEMONNIER qui m’invitait à participer à un groupe de réflexion académique sur la classe inversée ou plutôt « les classes inversées« .

J’ai mis un peu de temps à répondre à ce mail et j’ai fini par accepter, mais je ne me sentais pas vraiment légitime d’y être. Qu’est-ce que réellement la classe inversée (même si j’en proposais une définition et j’y émettais un avis il y a quelques années.)? Est-ce que j’en fais réellement ? J’ai accepté puis oublié pour profiter des vacances.

Bref, donc, jeudi m’y voilà. Un peu stressé. (Serais-je à la hauteur de l’attente, vais-je y trouver mon compte?).

Je fais donc parti d’un groupe d’une dizaine de personnes des enseignants lycée pro, lycée général, collège, d’IPR, représentant DAN,représentant CARDIE, formateur CAFFA, tous de disciplines différentes et d’horizons différents. Le groupe existe depuis 4 ans, nous sommes seulement 3 nouveaux. Et les personnes sont plutôt expertes en CI (Classe Inversée), les échanges furent rigoureux et les temps réflexions riches. Dommage que le temps de restitution-partage fût court.

Durant cette journée, nous avons dû émettre les axes de nos futurs travaux, je vais donc vous présenter le mien en redéfinissant ce qu’est ma classe inversée (on parle bien de classes inversées).

I. Ma classe Inversée

Alors, je suis parti sur le rejet complet de donner aux élèves à visionner les vidéos chez eux. Pour plusieurs points :

  • l’inaccessibilité au numérique (quoi qu’on en dise, il y aura toujours un ou deux élèves pour lesquels c’est compliqué, notamment au collège, soit par choix des parents : »pas d’écran le soir », soit par manque de moyen numérique ). D’ailleurs cette problématique est surtout présente au collège.
  • Le glissement possible vers un cours 100% frontal, où la découverte de notion passe par la vidéo me dit qu’on fait ça, donc je fais ça. Ce qui ne veut pas dire que le cours frontal soit tout le temps inadéquat, mais il est rarement pertinent (forme de diaporama commenté) sauf quand la vidéo est modélisante (qui montre que le numérique peut être un réel atout pour la compréhension de nouveau concept).

J’ai donc pris la liberté de redéfinir la classe inversée comme étant un cours où un moment est inversé temporellement ou personnellement. Cette définition me paraît pertinente et englobe tout type de classes inversées possibles.

La classe inversée dont le cours est donné aux élèves sous forme de capsules en fait parti puisque le moment d’apport de nouvelles notions est inversées temporellement avec celui des exercices à faire.

Mais l’inversion peut également être dans la relation connaissance-support-personne.

Je m’explique.

Moi, je compte inverser le moment lié à la trace écrite, celle que l’élève met dans son classeur pour se souvenir des connaissances.

Dans un cours classique (ou normal, dans le sens « normé »), l’enseignant produit une trace écrite au tableau que les élèves copient, ou photocopie un cours, ou même un texte à trous, bref, ici la trace écrite est cadrée fortement par l’enseignant. Voici un schéma de la transmission de la trace écrite.

blank

La connaissance est modelée par l’enseignant sous forme de trace écrite.

L’idée est donc d’inverser les rôles. Proposer aux élèves de créer leurs propres traces écrites en fonction des connaissances qu’ils auront acquises. On pourrait résumer avec ce schéma :

blank

Rapidement, on pourrait penser à de la classe dialoguée : « bon, les 3emes, j’écris quoi pour résumer telle notion« , sauf qu’il n’en est rien, je parle bien de l’élève seul.

Ici, mon hypothèse de base est que l’élève construise sa trace écrite personnelle sous n’importe quelle forme et que l’enseignant puisse s’en servir pour comprendre l’élève.

II.L’expérimentation : mise en place.

Plusieurs problèmes se dégagent :

  • Quel apport de connaissances et sous quelle forme ?
  • Quelle place du numérique ?
  • Comment vérifier la conformité de la trace ?
  • Comment aider les élèves à faire leurs traces sans la normaliser ?

J’y réponds normalement en tout point reste à prouver l’efficacité d’inverser ce moment par un essai (en fait 3, puisque j’ai 3 classes de 4emes)

Alors tout d’abord, je me sers d’un premier dispositif que j’ai mis en place depuis 3 ans, le livret de connaissances.

Dans ce livret, on retrouve en 4eme, la totalité des nouvelles connaissances et des connaissances de 5eme. Ils ont donc un cours officiel non résumé qui correspond exactement à ce que je veux puisque je l’ai fait.

  • blank
  • blank

J’ai expliqué aux élèves que nous allions concevoir des fiches qui résumerait les connaissances découvertes et ce dont ils ressentent en avoir besoin. Cette fiche est résumé une feuille A4.

Sur cette fiche, je leur donnerai à coller une entête de ce type :

blank

On retrouve :

  • les objectifs du chapitre : ce que doit maîtriser les élèves en termes de connaissances.
  • La référence au livret, si problème de connaissance, on regarde à la page du livret (on facilite l’accès aux connaissances). Ce sont des ressources non-numériques.
  • Un QR-Code qui mène à une version numérique du livret agrémentée de vidéos, QUIZ, exerciseurs, jeux. Ici, ce QR-code mène là. Cette diversité de ressources choisies permet aux élèves de conforter leur modèle qu’ils ont construit autour de la notion.

Ils ont donc à disposition des ressources et un cours « officiel » (qui ne l’est pas pour eux, car ils n’ont pas écrit. Un élève pense souvent à tort que parce que ça n’est pas écrit, ce n’est pas à savoir.)

Ce que j’attends des élèves.

Au moment,où l’on validera un objectif en découvrant une notion, je demanderai aux élèves de créer leur trace. Je laisserai un temps pour le faire (et aussi le terminer chez eux si besoin).

Pour l’instant, mes deux premiers chapitres, j’ai guidé les traces écrites en en proposant une au tableau (en leur disant de ne copier que ce qu’ils voulaient). J’ai proposé des exemples types pour l’un et une carte mentale pour l’autre, afin d’élargir le champs des possibles dans les futures fiches.

Je rends donc autonome (ou j’essaie, ne soyons pas pompeux) les élèves sur la trace écrite qui force une appropriation du cours : pour résumer, je dois forcément comprendre ce que je fais.

Et enfin, dernière subtilité, au moment des contrôles, je récupérerai les fiches des élèves. En cas de mauvais résultat :

  • si c’est un problème de fiche
    • soit mauvaise compréhension de la notion et donc c’est à moi d’agir (En apportant d’autres ressources, ou avec une remédiation par pair etc… les dispositifs sont divers et variés)
    • Soit un problème pour créer la fiche, donc c’est toujours à moi d’agir (là on peut travailler sur la trace écrite, cela reste complexe car il faut éviter la normalisation)
  • si c’est un problème d’apprentissage
    • à lui d’assumer cette tâche… quoique pour certains élèves la notion d’apprendre peut être complexe et nécessite un accompagnement

L’idée est en fait d’entrer dans la tête des élèves de savoir comment il procède et assimile les notions, de les rendre autonomes.

Alors j’ai appris également lors de la réunion, que si c’était une inversion en classe, alors on parlait plutôt de classe renversée. Bon, « renversée« , « inversée », l’idée est que l’élève lui soit au cœur du processus de ma réflexion.

C’est aussi la fusion de 3 projets-réflexions : cours interactifs, livret de connaissance et conception de fiches et enfin des contrôles grattés.

On verra pendant l’année ce que je vais retirer de l’expérimentation.

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

Bilan sur l’évaluation globale par compétences

Bon, ça faisait un moment que ça me trottait dans la tête que certains me l’avait demandé donc je m’y mets !

Evaluation par compétences.

Alors cela fait maintenant 2 ans que le collège est passé au 100% compétences (et 10 ans pour moi) avec une liste commune d’une cinquantaine de compétences qui sont toutes transdisciplinaires. L’idée à l’époque était de coller au socle commun et également de produire une grille de compétences lisible et synthétique.

Il fallait donc un nombre restreint de compétences mais qui permette toujours de fournir un portrait scolaire de l’élève. Cette année, la liste n’a pas évoluée (enfin si, on a cassé une compétence en 2 compétences), c’est donc qu’on est arrivé à maturité sur cette réflexion et ça c’est plutôt cool.

On est plutôt content d’évoluer par compétences et revenir en arrière est exclus pour quasiment tous les profs (un seul souhaite potentiellement le retour).

Quid de l’élève?

C’est là que le bas blesse ! J’en ai été franchement gêné cette année voyant le non sens que cela pouvait avoir pour les élèves. Que faire d’un « modéliser » non acquis, est-ce que l’élève saura quoi en faire? La réponse est non.

Alors au début, je me suis convaincu que mon appréciation sur les devoirs suffirait à aiguiller l’élève… En fait non.

L’élève, lui, ne regardait le nombre de point rouge et de point vert et s’enorgueillissait d’avoir plus de vert qu’avant sans pour autant juger si réellement il y avait progression ou non.

Ce travers, je l’ai perçu assez tôt et pourtant avant quand j’évoluais par objectifs (je m’appuyais sur des savoirs-faire), les élèves s’intéressaient sur quels types de points vert ils avaient.

J’en ai conclus que l’évaluation par compétences n’était plus au bénéfice de l’élève au moment de la restitution de l’évaluation… Au mieux, elle nous servait à nous professeur.

J’en étais à me dire qu’il fallait retourner en arrière (vers de l’évaluation par objectifs notionnel), sauf que si toutes les disciplines s’y mettaient, on explosait le compteur de « compétences » (entre guillemets car ce sont des savoirs-faire et non des compétences).

La solution est venu d’une idée de ma collègue Charline.

Elle a repensé la cartouche de l’évaluation, on passe donc de :

blank
Cartouche 2018

à

blank
Cartouche 2019

Donc on continue d’évaluer par compétences globales en mathématiques avec ces 10 compétences :

  • Mémoriser
  • Chercher
  • Calculer
  • Modéliser
  • Représenter
  • Communiquer
  • Écoute et respect des autres
  • Travail en équipe
  • Travail personnel et organisation
  • Participation, implication, prise d’initiative et autonomie

Et on ajoute une grille d’acquisition de notions que l’on pointera et donc l’élève de manière synthétique pourra voir quoi travailler, et ce qu’il maîtrise.

L’élève aura, également, un tableau sur son classeur où il indiquera son suivi de validation de notions.

Nous, professeur, on aura le tableau de validation des compétences qui rentrera sur le bulletin.

On espère ainsi que l’élève saura quoi travailler ce qui est le plus important quand même, non?

Et pour les compétences transversales, on fera juste un bilan en mi semestre et fin de semestre de ce type :

blank

Bref, je pense que là le système aura du sens, reste à expérimenter! 🙂

Pour ceux que cela intéresse, voici notre grille de compétences pour tout le collège

et sinon les échelles descriptives pour les compétences :

Je sais…
Niveau débutant
Niveau apprenti
Niveau confirmé
Niveau expert
Mémoriser
Restituer une partie des attendus Restituer tous les attendus Restituer les attendus de manière claire
Chercher
Trouver une information dans un document simple, m’engager dans une démarche Extraire les informations utiles, repérer ce que je cherche Extraire toutes les informations utiles, les reformuler et les organiser Exploiter les informations, me diriger vers les bonnes idées
Raisonner Faire des essais Utiliser, faire des essais pour proposer une méthode de résolution Proposer un raisonnement cohérent, analyser et exploiter mes erreurs Valider mes résultats par des raisonnements et démontrer
Calculer Refaire une technique de calcul avec un modèle, donner un ordre de grandeur Mener un calcul simple sur des nombres de manière exacte ou approchée Mener un calcul complexe en combinant calcul mental, calcul posé et instrumenté Calculer sans erreur, utiliser le langage algébrique (lettre, symbole)
Modéliser Faire le lien entre une situation réelle et un modèle simple Traduire un problème en un modèle théorique (croquis, schéma, représentation) avec une aide Traduire, seul, un problème en un modèle théorique (croquis, schéma, représentation) … et critiquer un modèle donné
Représenter
Identifier le mode de représentation à utiliser (graphique, schéma, carte, dessin) Réaliser une représentation incomplète, imprécise (main levée, mais codée) ou avec de l’aide Réaliser une représentation complète précise (avec instrument) sans aide Optimiser, choisir et critiquer une représentation
Communiquer Ecrire des calculs, faire des figures ou des graphiques. Expliquer oralement ma démarche. Détailler les étapes, expliciter mes résultats ou ma démarche à l’écrit ou à l’oral Utiliser les notations, le vocabulaire mathématique à l’oral ou à l’écrit Rédiger mon travail, argumenter mes résultats, écrire les règles ou propriétés utilisées
Programmer Exécuter un programme sur papier Corriger et analyser un programme Concevoir ou analyser un programme simple Concevoir un programme complexe

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

L’introduction de la lettre : la ligne brisée.

Salut à tous!

Bon je reviens d’une formation sur le calcul et la résolution de problème où j’ai pu revoir avec plaisir des camarades de l’université (super content de t’avoir revu Laorans). 🙂 Une belle journée!

blank

Allez, zoup ce soir, je m’essaye à proposer ma manière d’introduire la lettre au cycle 4 de manière efficace.

J’introduis en douceur cette notion sur du long terme (dès septembre pour commencer réellement en février), je ne l’intègre pas dans un « chapitre », disons que je commence la séquence officiellement au moment où tout est déjà fait.

Je pose, en quelques sortes, mes petites graines lors de l’activité mentale de début d’heure (que je fais à tous les cours).

L’idée est de partir sur la ligne brisée (un dessin rapide) et on demande la longueur de cette ligne.

Alors généralement mon premier dessin au tableau ressemble à celui-ci.

blank

En fait, je le fais à l’arrache mais du même type, je pense que de ne pas le préparer réellement, l’élève se dit que ça va être simple car sinon le prof l’aurait fait proprement… je vous jure que l’impression est différente.

La première fois, il y a un vrai blocage (lié au blanc) il y aura des contestataires, des gentils qui diront que c’est incomplet ou que c’est impossible ou ceux qui pensent trouver une solution proposent 13 ou 5+6+2.

Alors là, c’est le moment de les taquiner : « Ah bon? Rien ne vous gêne?« .

« Bah si, on connaît pas tout, c’est impossible en fait!« 

A vous de répondre que même la mémé du coin (moi j’aime bien la mémé de Loué, elle est rigolote) elle sait exprimer la longueur de cette ligne brisée, car elle la décrit simplement.

Si personne ne propose un truc satisfaisant pas grave, on imite la mémé (côté théâtral pour marquer les esprits, ça aide)

« Vind’iou , ça fait : un truc + 13 !! »

La réaction des élèves sera immédiate : « Ah d’accord, bah on savait pas qu’on pouvait etc… » . À ce moment là, il faut les autoriser à faire ce qu’ils veulent, leur dire d’oser… et proposer d’autre expression pour désigner l’espace vide « truc » « machin » « bidule »… puis passer à autre chose, notamment le cours que vous aviez prévu (sur une autre notion). On laisse digérer cette information.

Le cours d’après (on a laissé mariner cette découverte), on propose un autre dessin :

blank

Ici, on aura les erreurs du type : « 2 trucs +12 »

Des élèves devraient remarquer qu’il n’y a pas de codage donc de proposer une autre expression « truc + machin +12« . Un vrai débat peut s’installer, super riche.

Ensuite, d’autres dessins en vrac pour progresser sur la modélisation d’une longueur avec des inconnues. Il s’agit d’en faire plusieurs fois sur du long terme.

blank

On aura des réponses du type :

  • truc+4+truc+machin+6
  • truc+truc+machin+10
  • 2 trucs+ machin +10

Il suffira d ‘entourer que :
truc +truc = 2 trucs

blank

On teste leur imagination pour nommer des inconnues différentes, ça va coincer, comment faire autrement? La lettre comme outil rapide truc devient t, machin m, bidule b et donc il reste plein d’autres lettres.

blank

On peut également travailler sur la réduction de somme car on peut attendre deux types de réponses :

  • 2+3+x+x+x+y+y
  • 5+3x+2y
blank

La distributivité, on la reconnaît non?

Ici, on peut attendre 4(3x+5) ou 12x+20

blank

On peut également recontextualiser à posteriori sur les erreurs du type :

4x+2=6x

Bref, la ligne brisée permet de visualiser rapidement des manipulations avec le calcul littéral. Elle permet visuellement de déconstruire des erreurs et rapidement corriger le tir.

Toutefois, elle ne permet pas tout, comme on ne peut pas arriver à gérer la multiplication (sauf avec un scalaire), mais pour débuter sur le calcul littéral (dans le sens manipulation et modélisation) c’est sympa, non?

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

Le statut du signe =, l’égalité des produits en croix, un exerciseur…

Cette année, j’ai changé ma progression en 4eme pour coller à un EPI. Au lieu de commencer gentiment par les relatifs, pif paf pouf, on commence par la proportionnalité.

Bigre, en fait, la proportionnalité avant je la préparais, j’anticipais l’analyse des situations de proportionnalité, la préparation au nouveau statut du signe ‘=’ (via mes questions flash de début d’heure). Sauf que là, la préparation n’a pu avoir lieu, il fallait que l’EPI (avec le sport sur la VMA) colle aux séances d’EPS.

J’ai largement sous-estimé cette impréparation pour le nouveau statut du signe ‘=’. Comme quoi, quand on s’enfonce dans une routine, on a tendance à oublier les écueils rencontrés.

I.Un constat.

Là, je me suis trouvé confronté à plusieurs problèmes :

  • le statut du signe égal incompris (le fait de transformer une égalité)
  • ce que signifie l’égalité des produits en croix (parents, prof de physique vont souvent à contre sens)
  • l’aversion à la rédaction

Bref,pour ces deux derniers points, j’en avais toujours conscience, d’ailleurs ça prend plus ou moins de temps avec les élèves, je reste inflexible, j’argumente et ça passe.

Par contre, pour ce signe égal… Le passage entre ces deux lignes n’est pas aussi évident et se faisant, la pression donnée par l’EPI (où il fallait passer par là), il fallait l’utiliser forcément sous peine de légitimer une rédaction bancale ( afin d’éviter ce genre de propos » Ouais avant on faisait ça en EPI, pourquoi plus maintenant?« ) :

4 \times 5=3 \times x \newline 20=3 \times x \newline {20 \over 3}=x ou x={20 \over 3}

Au lieu de cela je me suis trouvé confronté à ce genre de rédaction:

4 \times 5=3 \times x \newline 4 \times 5=20 \newline 20:3={20 \over 3} \newline x={20 \over 3}

Ici, on se rend compte que la position du signe égal est en faveur du calcul, de la simple opération.

Alors bien entendu, c’est un travail de longue haleine par lequel je reviendrai avec Pythagore, Thalès et les équations. Mais d’avoir autant d’opposition dès le début, j’ai oublié qu’avant insidieusement et quasi-inconsciemment, je le préparais.

D’ailleurs en commençant le théorème de Pythagore, j’ai, pour une classe rapidement, donné un exemple d’utilisation (et de rédaction), un élève est venu me voir en disant que c’était comme l’égalité des produits en croix (Merci Noam!). Au début, je n’ai pas compris son allusion.

En fait, il parlait de la rédaction, le fait de transformer l’égalité. Bref, il avait compris mais n’avait pas su le verbaliser.

Sinon j’ai eu ce genre de rédaction

x = {{4 \times 5} \over 3} \newline x={20 \over 3}

Ici, on est sur l’ordre de l’astuce, du ‘truc’ qu’on comprend pas trop, mais ça marche.

On évite soigneusement tout le travail sur l’égalité, c’est aussi pour cela que je m’y oppose fermement. Car sinon, on reporte ce problème sur le théorème de Pythagore où on aura d’autres problèmes à gérer…

II. Quid de ce constat?

Alors, je me suis demandé comment j’allais raccrocher les wagons avec ceux où cela ne faisait pas sens.

Je me suis rappelé d’un propos d’une formatrice (Pascal Boulais, il y a… 10 ans… oui, je sais…), parfois le sens peut venir après le contrôle mécanique de la notion. C’est-à-dire qu’un élève peut très bien maîtriser une rédaction ou un concept et comprendre le sens seulement après utilisations. Cela ne doit pas poser de problème car les élèves ne sont pas forcément tous prêts à prendre du recul sur ce qu’ils font.

Elle faisait le lien avec les fameux « déclics » que des élèves souvent en 4e ont : « Ah mais ouiiiiii, ca y est je comprends, vous expliquer mieux que Machin l’an dernier » (alors qu’en fait, tout simplement, il n’avait pas le recul nécessaire).

(D’ailleurs serait-ce un déclic de ma part par rapport à cette phrase? 😉 )

blankDonc, fort de cette analyse (bonne ou mauvaise), j’ai conçu un exerciseur pour « forcer » à travailler cette rédaction liée à la transformation des égalités (sur la notion des produits en croix).

Bon, il analyse plutôt bien. Il est encore tatillons sur certaines rédactions, car c’est dur d’être exhaustif.

Il accepte toutefois plusieurs rédactions (allant cette à 4 étapes, 3 étapes, voir deux étapes et il te dit gentiment que c’est court quand tu utilises directement x=a*c/d )

Il s’agit d’une première version. Il est possible que j’implémente la possibilité de passer par le coefficient de proportionnalité ou l’addition soustraction des colonnes.

Ça se passe par là :

https://www.mathix.org/produits_en_croix/

 

Il suffira de mettre ce code sur votre site pour l’intégrer :
<iframe src="https://mathix.org/produits_en_croix" width="934px" height="555px"></iframe>

Maintenant y a plus qu’à tester!

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

Mutualisons, partageons et régalons-nous!

L’épilogue d’un début d’une chouette aventure qui démarre enfin!!

Alors pour un rattrapage sur l’histoire, tout démarre chez Claire Lommé une super warrior de collègue de Maths, elle s’est mise en relation avec une centaine de collègues et s’est mise à partager ses ressources, les collègues en ont fait autant, bref, une super banque de ressources à disposition.

J’ai demandé à en faire partie, bah vi quand même c’est chouette, et puis vient la mise en ligne de mes ressources dans son google drive, sauf qu’il est au bord de la saturation et avec des vidéos ça ne l’aurait pas du tout fait….

Je lui propose de passer sur mon serveur, elle accepte, je transfère les 4 Go de données. Et puis je me rends compte que des ressources sont des scans de livre scolaire, donc on a monté une petite équipe de fou-furieux pour trier tout ça :

Claire Lommé, Claude Fey, Joan Riguet, Mickaël Noel et Richard Cauche.

Des noms que vous reconnaîtrez, car certains ont déjà partagé des ressources ici. 🙂

Bref, après 3 jours de tri intensifs, à se tirer les cheveux, à se faire des blagues, à citer Kaamelott, les tontons flingueurs, l’ensemble est organisé.

Donc comment ça marche tout ça?

Il faut aller ici, pour accéder aux ressourcesblank

Si vous voyez des ressources qui ne devraient pas y être, (problème de droit d’auteur) c’est qu’elles sont passées au travers de notre tri, merci de nous le dire, on l’enlèvera de suite.

Bref, régalez-vous!!

Et si vous souhaitez donner votre pierre à l’édifice, c’est simple. Il faut le déposer sur le DEPOT.

C’est par ici que ça se passeblank.

On triera ensuite pour le mettre dans l’espace PUBLIC. On souhaite éviter les fausses manip’ c’est pour ça que vous en pourrez pas les mettre directement dans le dépôt PUBLIC.

Vous retrouverez les accès sur la gauche!

blank

En tout cas, merci à l’équipe de fous!

Claire Lommé, Claude Fey, Joan Riguet, Mickaël Noel et Richard Cauche.

Merci encore Claire pour ta confiance!

 

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

Le QR-code une manière de rendre interactif les cours?

Bonjour à tous!

blankUne petite présentation d’une petite nouveauté que j’ai mise en place dans mes cours et ce, assez facilement.

Alors cette idée, je la tiens d’Aurélien Piétot, un copain, prof de maths, qui m’a présenté le travail de Gilles Tisseraud (Professeur des écoles) qu’en fait j’avais déjà croisé, il y a quelques années. Gilles avait fait des Mathaloué dans sa classe et m’avait convié une matinée dans son école.

Alors que viennent faire les QR-codes par là?

Et bien si vous vous souvenez, on a mis en place les livrets de connaissances en 4e et 3e afin que les élèves apprennent à chercher les informations et centrer l’activité en classe dans la rédaction autour de la résolution de problèmes. Mais j’avais deux handicaps qui arrivaient naturellement.

  • Impossible d’ajouter des exemples, y mettre de la couleurs etc…. le livret reste une connaissance « fixe » ,  difficile à annoter.
  • Impossible de rendre interactif, pas de son, pas de vidéos, pas d’exerciseurs…. Bref, une connaissance « statique », c’est aussi gênant avec ou sans livret.

I. Les « applications ».

blankPour combler l’impossibilité d’annoter le livret, j’ai mis en place dans les « classeurs », une partie « applications » (d’autres de mes collègues l’appellent aussi « fiches »).

A l’intérieur, j’y met si j’en ressens le besoin, des exemples types que nous rencontrons durant des exercices que nous effectuons ou lors de questionnement d’élèves : « M’sieur je ne comprends pas cette étape… »

Il n’en reste pas moins que je ne trouvais pas cela très satisfaisant. J’avais développé un livret numérique qui reprenait leur livret de connaissance avec des ajout de vidéos & exerciseurs… Un livret numérique qui permet aussi d’oraliser des exemples et sont, je pense, plus accessibles pour certains élèves.

Mais je rencontrais une grosse barrière, il fallait soit l’ordinateur, soit la tablette, et cliquer sur le site du collège, puis l’icône du livret numérique, puis choisir « 4e » puis « chapitre relatifs » . ARGGG! Trop long, trop complexe !!!

II. Les QR-Codes.

blankSuite à la discussion avec Auré’, ça a été rapide dans ma tête, il faut des QR-Code à scanner, on peut imaginer des élèves avec leurs smartphones lorsqu’ils veulent plus de précisions scanne le QR-Code.

Je dis bien, j’imagine, car j’expérimente que depuis cette année. Le retour immédiat a été très positif auprès des élèves. Certains m’ont fait part de leurs tests.

Mon petit moins pour l’instant est que peut-être je devrais faire des QR-Code qui pointent directement sur une vidéo plutôt que le chapitre du livret numérique…. Je ne sais pas trop.

 

 

 

 

 

 

III. Créer des Qr-codes facilement.

Alors les outils pullulent sur internet, je n’ai pas trouvé de quoi générer directement une plaquette de QR-Code.

Alors juste pour les 3% d’utilisateurs de linux, je propose un petit outil qui fait ça tranquillement.

Le programme : etiquette_qrcode

A dézipper et copier-le dans /usr/bin.

Installer aussi les programmes (généralement disponibles dans toutes les disitributions linux : zenity , imagemagik, qrencode)

Ensuite, ajouter une action personnalisée dans Xfce (Thunar).

blanket voilà.

 

Sinon pour windows  et bien je n’ai trouvé que des générateurs en ligne (plus pratique que les logiciels gratuits proposés), le plus sympa que j’ai trouvé après une maigre recherche :

http://fr.qr-code-generator.com

https://micetf.fr/qrcode/

Mais bon, il faudra dupliquer l’image, ou imprimer l’image avec windows et demander de faire de multiples copies sur la même feuille.

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

Une évaluation par compétences globales

Voilà! De retour de vacances bien reposantes! J’espère que pour vous ça l’a été!

Je vous laissais avant les vacances avec cette big news, comme quoi, on évaluait tous par compétence au collège. Et qu’on avait définit une grille de 50 compétences pour tout le monde. J’ai eu des questions de la part de collègues sur la faisabilité et aussi le pourquoi que 50 compétences et pas plus afin d’être plus précis. Ce questionnement, je l’ai eu aussi de la part d’un collègue qui vient d’arriver chez nous.

Je vais donc mettre en concurrence 3 systèmes d’évaluations, la chiffrée ( comprendre la note), l’évaluation par compétences de type items et l’évaluation par compétences globales (celle que l’on va faire cette année).

I. L’évaluation pour quoi?

D’abord pour comprendre notre réflexion, il s’agit donc de définir à quoi sert notre évaluation. C’est idiot, car je pense qu’on le sait tous un peu, mais afin de faire des liens avec la suite, je pense ce passage nécessaire.

L’évaluation sert d’abord à l’élève pour se situer au regard :

  • des objectifs d’apprentissage qu’on attend de lui
  • de savoir ce qu’il lui reste à faire à issue de l’évaluation

Alors généralement, l’appréciation que l’on met sur l’évaluation  (tout système confondu) permet de répondre facilement à ces deux points.

En effet, généralement, notre appréciation se découpe en trois parties :

  • Un bilan général (Très bien, bon travail, bilan mitigé, des faiblesses … )
  • Un bilan détaillé sur les notions maîtrisées, ce qui a été bien fait
  • Une conclusion sur ce qu’il reste à faire (ce qui a été mal maîtrisé)

Donc en somme tout système confondu du point de vue de l’objectif d’une évaluation y répond.

Alors pourquoi plusieurs systèmes d’évaluation?

II. Savoir faire un bilan global de toutes les évaluations qui soit juste.

A. La note son apparition et son utilité

blankLa vraie problématique reste que si l’on fait plusieurs évaluations, il faut être capable de pouvoir en tirer un renseignement afin qu’au conseil de classe par exemple ou face aux parents capable de résumer une période de la scolarité de leur enfant.

La première astuce qu’on a trouvée a été de mettre une note, (pour le BAC d’ailleurs en 1890) afin de comparer les différentes évaluations entre candidats.

Puis ce système de notation a essaimé dans le secondaire, la note s’est propagée comme un outil pratique pour voir s’il y a une progression positive ou négative entre cette fois-ci les différentes évaluations d’un même élève. La moyenne,elle, est venue un peu plus tard comme élément de synthèse objectif (qui ne dépend pas de l’évaluateur).

Si bien qu’entre appréciation et note, il y a depuis  une coexistence du bilan global. On sait que 19/20 c’est très bien par exemple! Pire, la note a supplanté la lecture du bilan global de l’évaluation a contrario de l’appréciation. C’est un vrai défaut que je vois en la note, elle occulte l’appréciation. Nous y reviendrons un peu plus tard.

B. Vers l’évaluation par compétences de types items.

blankCe  système d’évaluation a été inventé en premier lieu pour contrecarrer un défaut de la note : la comparaison entre évaluation qui n’a pas lieu d’être sachant que les évaluations ne sont pas comparables du fait qu’elles ne portent pas forcément sur les mêmes notions.

Il permet aussi de répondre de manière plus synthétique à l’élève pour savoir ce qu’il lui reste à faire à issue de l’évaluation. (un des objectifs de l’évaluation)

La progression par items est visible de manière très efficace. Bref, le bilan est très précis, mais on perd la notion de globalité, entre 5 points verts et 4 points rouges qu’en dire? C’est moyen? C’est bien? C’est faible?

Bref, un peu comme un gros balancier, on est arrivé dans un excès de précisions qui à perdre du sens sur le bilan global.

D’ailleurs généralement, l’appréciation était redondante par rapport au bilan précis d’acquisitions des items (savoir ce qu’il lui reste à faire à issue de l’évaluation), c’est d’ailleurs ce qui la met en second plan. On retrouve le même défaut que celui de la note. L’appréciation est occultée or c’est pourtant, elle, la plus précise car on peut donner des priorités ou de l’importance sur certaines notions contrairement à d’autres.

D’ailleurs j’ai souvenir encore que l’année dernière certains collègues avaient remarqués cette redondance et se contentaient d’écrire en appréciation : « Toutes les compétences n’ont pas été acquises, certaines sont à retravailler. »

Bref, c’est exactement ce qu’il faut éviter. Et même si on préservait l’appréciation, le bilan des items est plus affriolant car plus simple d’analyse au premier abord pour l’élève, mais difficile de donner des priorités de révisions, de l’importance à certains objectifs.

En plus, imaginer qu’un collège entier choisisse d’évaluer comme cela, on se retrouverait facilement avec 400 items voir plus (j’en avais 70 pour juste le niveau 4eme en mathématiques par exemple). Le bilan général est impossible à faire que ce soit pour le professeur principal voir même les parents.

C. Redonner sa place à l’appréciation

blankÇa me parait plus sensé, l’appréciation permet de passer de vrais messages et est plus précise (pour peu qu’on s’y donne la peine d’en écrire des précises, on est d’accord!). Donc il faut trouver un système qui permette de voir la progression globale (et non par item) de l’élève tout en ne parasitant pas l’appréciation.

Mais comment préserver la progression de l’élève durant l’année, comment comparer les évaluations et ce de manière globale?

C’est là qu’intervient la notion de ce que j’appelle les compétences globales.

blankRéduire le nombre de compétences pour :

  • Les rendre interdisciplinaires, c’est un non sens d’évaluer la même chose dans deux endroits différents uniquement parce que les disciplines sont différentes.
  • Rendre plus lisible le bilan global pour les parents avec des compétences lisibles : des intitulés clairs.
  • Remettre plus avant des compétences liées au savoir-être (puisque moins de compétences, celles-ci apparaissent mieux), ce sont ces compétences que les parents recherchent : « Mon enfant est-il attentif? Apprend-il avec soin son cours? Est-il altruiste? Respectueux? … »

On retrouve donc ici deux avantages :

  • Celui où l’information quant aux objectifs à revoir est remise en avant par une appréciation plus visible
  • Une progression qui rend compte sur des compétences globales qui ont plus de sens, et qui donne une meilleure lecture par les parents.

Après, tout comme l’évaluation par compétences de type item, ce nouveau système va demander une phase d’apprentissage pour les parents et pour les élèves mais aussi pour les enseignants. En effet, l’appréciation aura plus d’importance, il faudra donc bien la construire, ce qui nécessitera je pense un peu plus de travail lors des corrections de copie et du remplissage du bulletin, mais tout ça au service de l’élève.

Pour moi, il n’y a donc pas de perte d’informations, mais justement une meilleure communication.

Alors je pense à certains collègues qui m’avaient soumis cet argument  :  » Avec ce système tu parasites clairement l’information : savoir ce qu’il lui reste à faire à issue de l’évaluation qui est plus accessible avec l’évaluation par items, tu parasites la remédiation ». Rah, la remédiation. Et bien en maths en tout cas, je suis parfaitement capable de me rappeler quels élèves ont des difficultés sur telles ou telles notions. D’ailleurs j’en parlais avec une amie professeur il y a quelques semaines, on a remarqué qu’on utilisait très peu voir pas du tout, l’outil informatique d’évaluation par item pour savoir quoi donner comme remédiation à tel ou tel élève.

Alors normalement l’argumentaire (toujours cette amie) se poursuit avec : « Comment font les disciplines qui ont tous les élèves? » Ah oui, nos chers collègues d’Arts-plastique ou d’éducation musicale. Quand je regarde les appréciations sur les bulletins, celle-ci s’attache surtout au savoir-être (attitude en classe) et quelques compétences artistiques globales ce qui correspond parfaitement à l’évaluation par compétences globales justement!

III. Vers l’évaluation par compétences globales.

Dernier argumentaire pour ce type d’évaluation est celui du conseil de classe, voir plutôt de l’orientation.

En fonction des notes dans chaque discipline on dégageait des profils scientifiques, littéraires, sportif, manuel, artistiques …. que ce soit de manière explicite ou implicite, on le fait pour savoir si l’orientation choisie par l’élève correspond à ces compétences qu’il a.

D’où l’importance de compétences globales qui soient interdisciplinaires et qui respectent les pôles. C’est pourquoi le socle commun n’est pas si mal fait car par exemple, pour le domaine 1, il a été séparé en sous-domaines  qui correspondent aux pôles.

Bref, ce système permet aussi une meilleure analyse de ce qu’est capable l’élève pour son parcours avenir.

Bref, il répond à des problématiques qui vont bien au delà de la simple évaluation.

Après je ne dis pas que ce sera simple à mettre en place cette année,

on risque d’essuyer pas mal de plâtres.

Et vous, vous en pensez quoi?

 

 

 

 

 

 

 

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons
par Arnaud Durand

A loué, on va vers du 100 % compétences sur tous les niveaux!!

En voilà une grosse news, hein?

Alors petit récap’ pour vous ! Il y a 3 mois, on s’est engagé, toute l’équipe de sciences, (Techno, maths, SVT et Physique-Chimie) à créer une grille commune de compétences plutôt courte et vraiment interdisciplinaire…

blank

9 compétences orientées sciences sont dégagées et 9 compétences transversales (vraiment toutes disciplines) sont fixées.

Cette année, ça a été la foire question « évaluation », certains faisaient 100% notes, d’autres 100% compétences et d’autres pour faire le lien entre les deux faisait les deux (en maths, on était dans la dernière catégories, arg….).

Bref, hyper content d’avoir trouvé un terrain d’entente sur une liste plutôt courte, on se dit : « Bon on partage aux collègues et on voit si ça prend ou pas« . Ca a mordu un peu mais sans plus.

Mon collègue de Techno qui faisait un temps partagé sur le collège de La Suze (eux ils font du 100% compétences depuis plusieurs années) me donne leur grille après accord de leurs collègues (un petit coucou à Gregory L qui serait super dans l’équipe du rallye ^^ ), j’y insère nos compétences à nous et vire celles qui ne servaient à rien en sciences et je balance à tous les collègues en disant voilà ce qu’on pourrait faire tous ensemble…

S’ensuit un travail de réflexion dans chaque pôle.

Et bim, 3 mois plus tard contre toute attente (l’administration n’y croyait pas vraiment et je commençais à douter), je présente la grille corrigée à tous les collègues pour une ultime modification et validation et transmission à l’administration qui était présente à la réunion. YEEEEEEEES !!!!!

50 compétences validées pour tout le collège…

Quoi de mieux de vous la présenter!

Juste avant je vous dis juste …. BONNES VACANCES (même si, je compte encore publier un peu d’autres trucs, comme les projets prévus l’année prochaine ceux qu’on a testé en toute fin d’année, le reste des PB DUDU non encore montés etc…)

Vous avez aimé cet article ? Alors partagez-le avec vos amis en cliquant sur les boutons ci-dessous :

Licence Creative Commons